Свойства частости.

1.

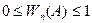
2. Частость достоверного события равна 1. W_n(U)=1.

3. Частость суммы попарно несовместных событий равна сумме частостей.

Рассмотрим систему A_i, i=1, ..., k; события попарно несовместны, т.е.

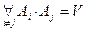Событие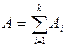

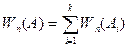
Пусть в результате некоторого испытания произошло событие A. По определению сумы это означает, что в этом испытании произошло некоторое событие A_i. Так как все события попарно несовместны, то это означает, что никакое другое событие A_j (i¹j) в этом испытании произойти не может. Следовательно:

n_A=n_A1+n_A2+...+n_Ak

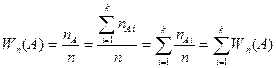
Теория вероятности используется при описании только таких испытаний, для которых выполняется следующее предположение: Для любого события A частость наступления этого события в любой бесконечной серии испытаний имеет один и тот же предел, который называется вероятностью наступления события A.

Следовательно, если рассматривается вероятность наступления произвольного события, то мы понимаем это число следующим образом: это частость наступления события в бесконечной (достаточно длинной) серии испытаний.

К сожалению, попытка определить вероятность как предел частости, при числе испытаний, стремящихся к бесконечности, закончилась неудачно. Хотя американский ученый Мизес создал теорию вероятности, базирующуюся на этом определении, но ее не признали из-за большого количества внутренних логических несоответствий.

Теория вероятности как наука была построена на аксиоматике Колмогорова.