Уравнение Шредингера

Мы уже разобрались, что состояние микрочастицы не может быть охарактеризовано совокупностью координат и проекцией импульса, как в классической механике. Так что же тогда отражает состояние микрочастицы? Шредингер предположил, что существует некоторая функция координат пространства и времени 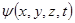, которая и является искомой характеристикой состояния микрочастицы. Он назвал ее волновой функцией и предложил уравнение для ее отыскания:

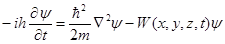, (13)

где 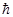- квант действия;

;

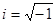m – масса покоя микрочастицы;

Ѳ - оператор Лапласа;

;

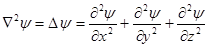W(x,y,z,t) – потенциальная энергия микрочастицы во внешнем силовом поле; если микрочастица свободна, то W(x,y,z,t)=0.

Отметим особенности уравнения Шредингера:

1. Это уравнение – дифференциальное уравнение частных производных, хорошо известное как волновое уравнение; его решением являются функции, описывающие процесс распространения волн в пространстве.

2. Уравнению () могут удовлетворять только комплексные значения. Поскольку комплексные числа – это математическая абстракция, не имеющая физического смысла, то и волновая функция y тожже не имеет физического смысла и значит, сама по себе не характеризует состояние микрочастицы.

Но оказывается, что физический смысл имеет произведение волновой функции y и комплексно сопряженной с ней функции :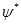

y y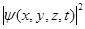^*= . (14)

Физический смысл произведения yy^* заключается в следующем:

Это произведение есть действительная функция, численное значение которой для данной точки пространства в данный момент времени, равно вероятности нахождения микрочастицы в единичном пространстве окружающем данную точку.

Эту вероятность обозначают W(x,y,z,t).

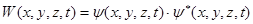(15)

или сокращенно

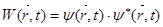. (16)

В соответствии с таким физическим смыслом волновая функция должна быть непрерывной и иметь непрерывную первую производную, однозначной и конечной во всех точках пространства, т.к. вероятность нахождения микрочастицы не может быть величиной неоднозначной, бесконечной или скачкообразно изменяться от точки к точке.

Отметим, что если мы рассматриваем поведение не одной, а совокупности (или системы) микрочастиц, то оно описывается их общей волновой функцией, зависящей от координат всех частиц. Например, для ситстемы из двух микрочастиц волновая функция имеет вид:

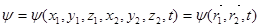, (17)

где x₁, y₁, z₁ – координаты первой микрочастицы;

x₂, y₂, z₂ - координаты второй микрочастицы.

Произведение 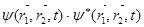имеет смысл вероятности того события, что в момент времени t одна из микрочастиц находится в единичном объеме, окружающем точку с координатами x₁, y₁, z₁ , а другая – в единичном объеме, окружающем точку с координатами x₂, y₂, z₂.

Потенциальная энергия, входящая в уравнение Шредингера, является в общем случае функцией координат и времени. Однако во многих практически важных задачах потенциальная энергия является функцией только координат и не зависит от времени. Для таких задач волновую функцию можно представить в виде:

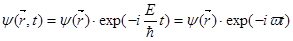, (18)

где Е – полная энергия микрочастицы.

Функция 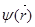, зависящая только от координат, называется амплитудой волновой функции. Ее можно найти из уравнения

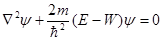, (19)

которое называется амплитудным уравнением Шредингера.

Силовое поле, в котором потенциальная энергия микрочастицы не зависит от времени, называется стационарным. Состояния микрочастиц в стационарном поле называются стационарными состояниями. Т.е. амплитудное уравнение Шредингера описывает стационарные уравнения микрочастиц.

Каждое состояние микрочастицы описывается одной волновой функцией. Если уравнение Шредингера допускает решение в виде нескольких волновых функций, то это означает, что микрочастица может находиться в нескольких различных состояниях.