Уровень Ферми

Вероятность нахождения электрона на том или ином энергетическом уровне при температуре Т определяется функцией Ферми – Дирака:

где W_F – энергетический уровень, называемый уровнем Ферми.

При Т=0°К вероятность занятия электронами уровней W > W_F равна нулю:

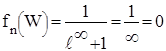
а уровней W < W_F единице: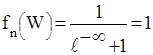

Энергия для перахода в зону проводимости берется от тепловых колебаний. Поэтому при Т=0°К свободных электронов в полупроводнике нет (ни один уровень в ЗП не занят электроном), все электроны находятся на орбитах (в ВЗ), следовательно, энергетические ЗП соответствуют условию W > W_F, а энергетические уровни ВЗ – условию W < W_F. Это говорит о том, что уровень Ферми W_F расположен ниже «дна» ЗП W_П и выше «потолка» ВЗ W_В, т.е. в ЗЗ. На рис. 3 приведены кривые функции Ферми – Дирака.

При Т=0°К фуекция f_n(W) имеет ступенчатый характер. Вероятность занятия электронами уровней в ЗП = 0, а в ВЗ = 1.

При Т > 0°К появляется небольшая вероятность занятия электронами уровней в ЗП, а вероятность занятия уровней в ВЗ соответственно снижается.

Из формулы Ферми – Дирака видно, что при температуре, отличной от абсолютного нуля (Т>0), уровень Ферми – это такой энергетический уровень W = W_F, формальная вероятность заполнения которого электроном равна 0,5 (т.к. е° = 1).

Формальное потому, что уровень Ферми находится в запрещенной зоне и фактически не может быть занят электроном. Таким образом, конкретный смысл имеют только те участники кривой распределения f_n(W), которые расположены в ЗП и в ВЗ.

Кривая распределения Ферми – Дирака всегда симметрична относительно уровня Ферми. Из этого, в частности, следует, что в собственном полупроводнике уровень Ферми расположен посередине ЗЗ. При повышении температуры от нуля появляется определенная вероятность занятия электронами энергетических уровней в ЗП. Но при этом на такую же величину снижается вероятность нахождения электронов в ВЗ. Нетрудно видеть, что при симметричном размещении кривой распределения f_n(W) относительно уровня Ферми это возможно только в случае, если уровень Ферми будет находиться посередине ЗЗ.