Отделение корней
На данном этапе определяются те интервалы области изменения переменной x, в каждом из которых расположен один и только один корень уравнения (3.1). По сути дела на этом этапе определяются грубые приближения значений x с погрешностью, определяемой длиной каждого найденного интервала. Полностью автоматизировать процесс отделения корней, пожалуй, невозможно, так как в нем обязательно присутствует элемент субъективного, интуитивного подхода к решению задачи. Иногда, например, интервал, в котором расположен корень, удается получить из физической сущности решаемой задачи.
При выполнении этого этапа с использованием ЭВМ обычно проводится "табулирование" функции F(x, a1, a2, ..., ak), т.е. построение таблицы ее значений при различных значениях x, следующих друг за другом с некоторым шагом h:
| x | F(x) |
| x1 | F1 |
| x2 | F2 |
| . . . | . . . |
| xn | Fn |
где xi+1 = xi + h ; Fi = F(xi); i = 1,2,...,n-1.
Например, таблица значений функции x2 - 12 ln½x½ + 6 sin xна промежутке [1,10] c шагом h = 1 имеет вид:
| x | F(x) |
| 1.0 | 6.05 |
| 2.0 | 0.72 |
| 3.0 | - 3.99 |
| 4.0 | - 6.01 |
| 5.0 | - 1.03 |
| 6.0 | 11.75 |
| 7.0 | 28.42 |
| 8.0 | 43.74 |
| 9.0 | 55.79 |
| 10.0 | 67.72 |
В качестве границ искомых интервалов выбираются такие соседние значения x, в которых соответствующие значения F(x) имеют разные знаки, так как изменение знака функции на некотором интервале означает в силу ее непрерывности, что где-то в пределах этого интервала график функции пересекает ось абсцисс, т.е. уравнение F(x) = 0 имеет корень. В частности, на основании данных из приведенной выше таблицы можно сделать вывод, что уравнение x2 - 12 ln½x½ + 6 sin x = 0 на промежутке [1,10] имеет по крайней мере два корня: в интервале (2,3) и в интервале (5,6).
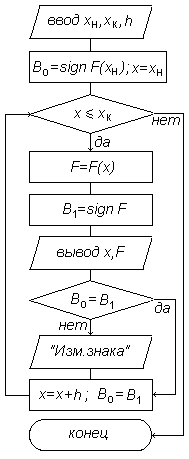 Рис.3.1. Алгоритм отделения корней
табулированием функции
Рис.3.1. Алгоритм отделения корней
табулированием функции
|
При выполнении этого этапа нужно проявлять определенную осторожность: во-пеpвых, одинаковые знаки функции F на концах интервала (xi, xi+1) не означают, что на этом интервале нет корней - их может быть, например, два; во-втоpых, при разных знаках на концах интервала здесь может оказаться не один корень, а три или, например, пять.
В приводимой на рис.3.1 схеме алгоритма отделения корней использованы следующие обозначения:
xН, xК - соответственно левая и правая границы промежутка табулирования функции F(x);
x - текущая точка табулирования;
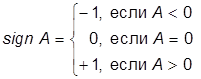 ;
;
В0, В1 - знаки функции F(x) соответственно в предыдущей и текущей точках табулирования.
В соответствии с данной блок-схемой производится не просто табулирование функции, а, кроме того, анализ знака функции в каждой новой точке и вывод сообщения при его изменении.
Дата добавления: 2015-02-16; просмотров: 1481;
