Метод простых итераций
Исходное уравнение (3.1) преобразуем к эквивалентному уравнению:
x = 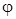 (x). (x).
| (3.8) |
Пусть известно начальное приближение (полученное, например, на этапе отделения корней): x = x 0. Подставим его в правую часть (3.8) и получим новое приближение: x1 = 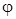 (x0). Повторяя эту процедуру, будем иметь в общем виде на некотором k-м шаге:
(x0). Повторяя эту процедуру, будем иметь в общем виде на некотором k-м шаге:
xk = 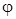 (xk-1) .
(xk-1) .
В качестве условия окончания вычислительного процесса можно взять выполнение неравенства: ½xk - xk-1½ < 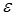 .
.
Значение xk, удовлетворяющее ему, и есть корень уравнения (3.1).
Геометрическая интерпретация этого метода приведена на рис.3.8, 3.9. Здесь x* - истинное, искомое значение корня; x0 - начальное приближение к корню; x1, x2, x3 - очередные итерации.
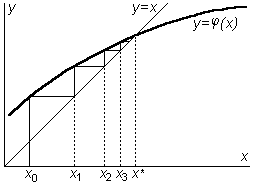 Рис.3.8.
Рис.3.8.
| 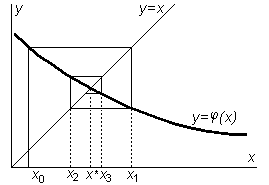 Рис.3.9.
Рис.3.9.
|
При использовании этого метода возникает вопрос о его сходимости. Дело в том, что при некоторых условиях расстояние между истинным корнем и приближениями к нему может возрастать с каждой новой итерацией, как это показано на рис.3.10, 3.11.
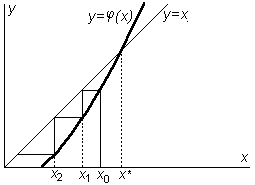 Рис.3.10.
Рис.3.10.
| 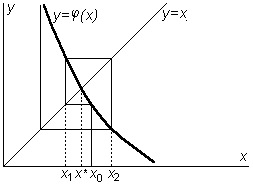 Рис.3.11.
Рис.3.11.
|
Условием сходимости метода простых итераций является выполнение в окрестности искомого корня неравенства:
½ 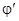 (x)½ < 1 (x)½ < 1
| (3.9) |
Это условие является достаточным, т.е. если оно выполняется, то процесс обязательно сходится; если же условие (3.9) не выполняется или выполняется не во всех точках
x0, x1, x2, ..., xk, ... ,
то заранее сказать что-либо конкретное о сходимости нельзя.
Итак, для решения уравнения F(x) = 0методом простых итераций надо преобразовать его к уравнению вида x = 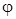 (x) так, чтобы выполнялось условие ½
(x) так, чтобы выполнялось условие ½ 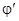 (x)½ < 1. Сходимость к истинному корню будет тем быстрее, чем ближе к единице значение
(x)½ < 1. Сходимость к истинному корню будет тем быстрее, чем ближе к единице значение 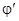 (x).
(x).
Дата добавления: 2015-02-16; просмотров: 759;
