Постановка задачи. Во многих инженерных и научных задачах возникает необходимость решения уравнений вида: F(x, a1

Во многих инженерных и научных задачах возникает необходимость решения уравнений вида:

где F - заданная непрерывная функция;

x – неизвестная величина, подлежащая определению;

a₁, a₂, ..., a_k – известные параметры функции F.

Решить уравнение (3.1) - это значит найти такое значение (или такие значения) неизвестной x, при которых уравнение (3.1) превращается в тождество. Эти значения x называются корнями уравнения (3.1).

Только для простейших уравнений удается найти решение в аналитическом виде, т.е. записать формулу

x = f(a₁, a₂, ..., a_k) ,

выражающую искомую величину x явным образом через параметры a₁, a₂, ..., a_k, например, для уравнения вида

ax² + bx + c = 0

его корни выражаются формулой:

.

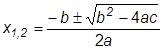В большинстве же случаев аналитическую запись корней уравнения найти очень сло­ж­но или в принципе невозможно (такие уравнения называются трансцендентными), и по­это­му приходится решать уравнение численным способом.

Существует несколько различных методов численного решения трансцендентных уравнений, но все они предполагают выполнение двух этапов: первый из них называется "отделение корней", второй - "уточнение корней". Ниже рассматривается один из спосо­бов отделения корней и четыре метода уточнения корней - метод дихотомий, метод хорд, метод касательных и метод простых итераций.