Пример 1.2

Имеется следующий ряд распределения семей по числу членов семьи:

Таблица 1.2

Число членов семьи ( )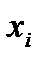
Число семей ( )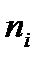

Здесь мода 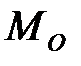=3 человека в семье, так как наибольшее число семей (500) в данном ряду имеют 3 человека в семье.

В интервальном ряду мода определяется по формуле:

,

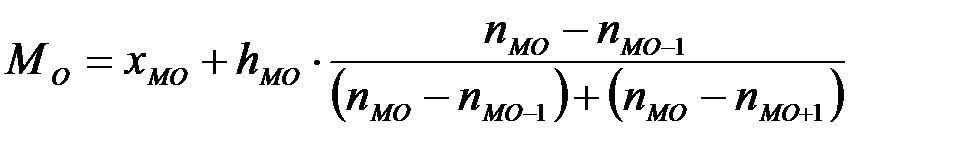где 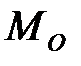- мода;

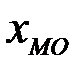- начальное значение модального интервала (интервала, содержащего наибольшую частоту);

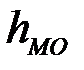- величина модального интервала;

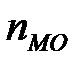- частота модального интервала;

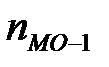- частота интервала, предшествующего модальному интервалу;

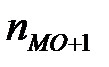- частота интервала, следующего за модальным интервалом.

Рассмотрим нахождение моды в интервальном ряду распределения по условию табл. 1.1.

В этой задаче наибольшая частота (12) находится в интервале от 500 до 700. Это модальный интервал. Тогда мода:

.

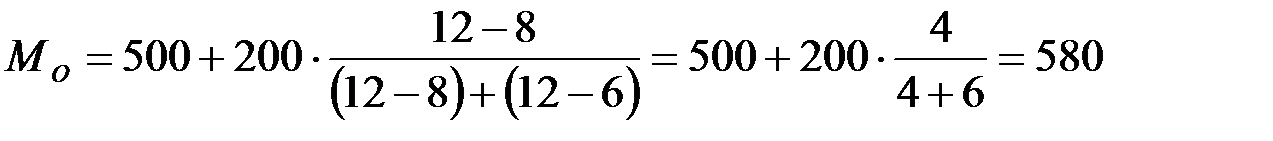Итак, модальная величина объема выполненных работ составляет 580 млн. руб.

Медиана - это вариант, расположенный в середине ранжированного (упорядоченного) ряда.

Ранжированным называется ряд, в котором единицы совокупности расположены в возрастающем (или убывающем) порядке значений варианта.

В дискретном нечетном (нечетное число единиц) вариационном ряду распределения медианой будет значение 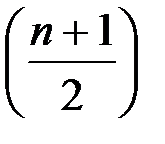- го варианта.

Например, при испытании прочности семи образцов стекла на силу удара в кг были получены результаты:

4, 5, 6, 7, 8, 8, 15.

В середине ранжированного ряда находится четвертый вариант и его величина есть медиана. Итак, 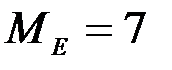кг или медианное значение прочности стекла при испытании на силу удара составило 7 кг.

В дискретном четном (четное число единиц) вариационном ряду распределения медиана находится как средняя из двух вариантов, расположенных в середине ранжированного ряда, т.е. среднее значение 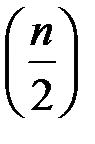- го и 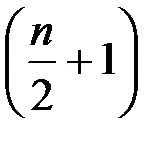- го вариантов.

Рассмотрим нахождение медианы в дискретном четном ряду распределения по условию табл. 1.2. Данный ряд имеет четное число элементов, так как

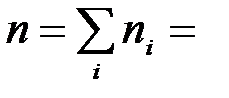300+500+260+100+40=1200, тогда в середине ранжированного ряда будут находиться 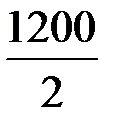-ый и ( 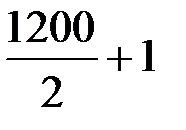)-ый варианты, или 600-ый и 601-ый. По суммам накопленных частот (см. табл. 1.3) видно, что и 600-ый и 601-ый варианты имеют значение 3. Значит медиана 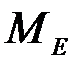=3 человека в семье.

Таблица 1.3

Число членов семьи ( )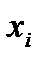
Число семей ( )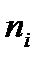
Сумма накопленных частот (S )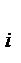

Медиана интервального вариационного ряда определяется по формуле:

,

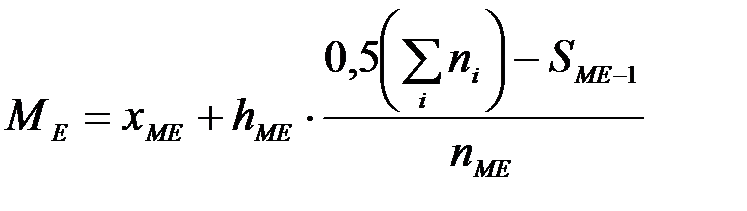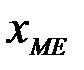- начальное значение медианного интервала (интервала, содержащего медиану);

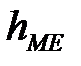- величина медианного интервала;

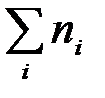- сумма частот ряда;

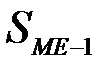- сумма накопленных частот, предшествующих медианному интервалу;

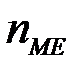- частота медианного интервала.

По данным табл. 1.1 найдем медиану.

Таблица 1.4

Группы предприятий по	Число	Сумма накопленных
объему выполненных	предприятий	частот
работ, млн. руб.	(n 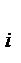)	(S )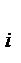
От 300 до 500
От 500 до 700
От 700 до 1000
От 1000 до 1300
Итого:		—

В данном примере в середине ряда находится варианты с порядковыми номерами 15 и 16. Медианным интервалом является второй – от 500 до 700.

Находим медиану по приведенной выше формуле.

.

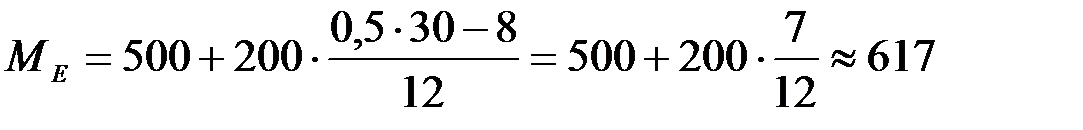Итак, медиальная величина объема выполненных работ составляет 617 млн. руб.