Пример 1.1
По строительным предприятиям области получены данные об объеме выполненных строительных работ за год (см. табл. 1.1).
Таблица 1.1
| Группы пред- | Расчетные показатели | |||
| приятий по | Число | закрытые | центральное | |
| объему выпол- | предприя- | интервалы | значение | x 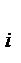 n n 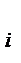
|
| ненных работ, | тий (n 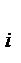 ) )
| по группам | интервала | |
| млн. руб | ( 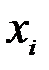 ) )
| |||
| до 500 | 300-500 | |||
| от 500 до 700 | 500-700 | |||
| от 700 до 1000 | 700-1000 | |||
| свыше 1000 | 1000-1300 | |||
| Итого: | — | — |
Вычислим средний объем выполненных работ на одно предприятие, используя формулу средней арифметической взвешенной.
Вначале закрываем интервалы. Исходя из того, что весь интервал второй группы равен 200, нижняя граница первого интервала будет исчислена: 500-200=300. Интервал предпоследней группы равен 300, тогда верхняя граница последнего интервала будет 1000+300=1300. В графе 3 все интервалы после этих расчетов записаны закрытыми. По формуле простой арифметической средней исчисленные центральные значения интервалов записаны в графе 4. Эти значения и будут служить вариантами ( 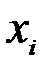 ) для расчета средней арифметической взвешенной
) для расчета средней арифметической взвешенной
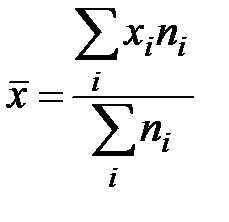 =
= 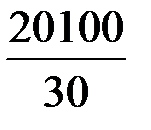 =670 (млн. руб.).
=670 (млн. руб.).
Средняя гармоническая:
простая
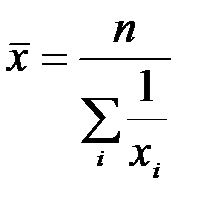 ;
;
взвешенная
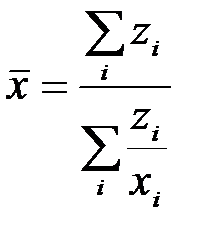 ,
,
где 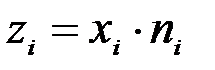 .
.
Приведем пример расчета средней гармонической. Допустим, что трое рабочих работали по 8 часов (480 мин.) и затрачивали на отделку 1 кв. м стен: 1-й – 30 мин., 2-й – 40 мин., 3-й – 60 мин. Найти среднюю затрату времени на отделку 1 кв. м стен по формуле:
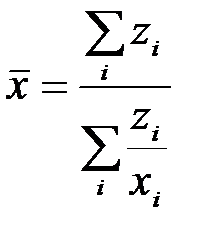
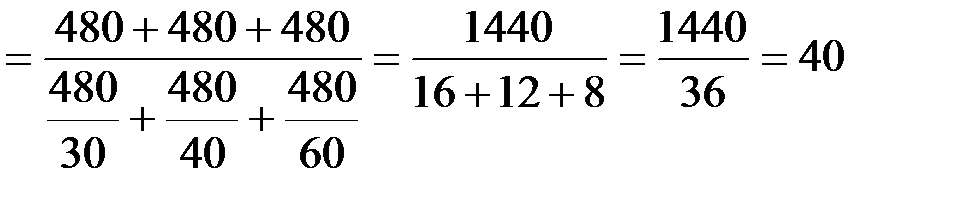 .
.
В этом расчете в числителе значится общее время работы трех рабочих (1440 мин.), а в знаменателе общее количество отделанных кв. м (36 кв. м). Средняя затрата времени на отделку 1 кв. м составляет 40 мин. В данном примере веса средней равные и поэтому можно записать:
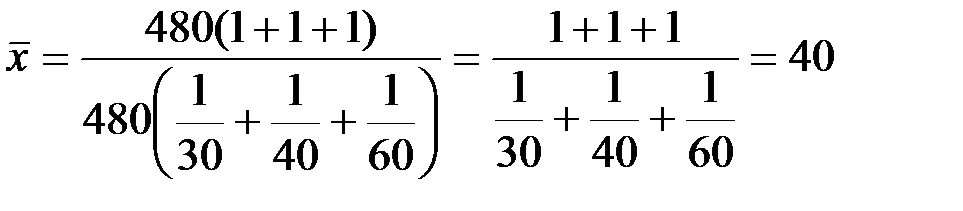 .
.
Следовательно, при равных весах расчет может быть произведен по формуле:
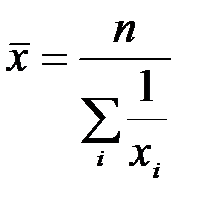 .
.
Средняя квадратическая:
простая
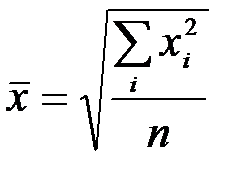 ;
;
взвешенная
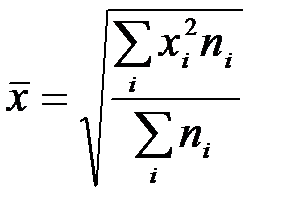 .
.
Эта средняя применяется при нахождении показателей вариации, которые рассматриваются далее, например, среднеквадратического отклонения.
Средняя геометрическая:
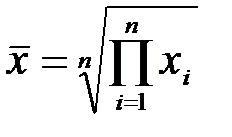 ,
,
Эта средняя применяется, например, при нахождении средних темпов роста в рядах динамики.
К структурным средним относятся мода и медиана.
Мода - это величина признака (вариант), который чаще всего встречается в данной совокупности.
В дискретном ряду распределения моду исчислять не требуется, она находится как значение варианта ( 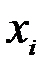 ), у которого наибольшая частота (
), у которого наибольшая частота ( 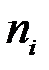 ).
).
Дата добавления: 2015-02-13; просмотров: 711;
