РЯДЫ РАСПРЕДЕЛЕНИЯ. СРЕДНИЕ ВЕЛИЧИНЫ. ПОКАЗАТЕЛИ ВАРИАЦИИ И ДРУГИЕ ХАРАКТЕРИСТИКИ РЯДОВ РАСПРЕДЕЛЕНИЯ. СТАТИСТИЧЕСКИЕ ГРАФИКИ

КРАТКАЯ ТЕОРИЯ.Рассмотрим движение твердого тела в жидкости или газе. Исходя из принципа относительности Галилея, безразлично тело движется с некоторой скоростью относительно покоящейся жидкости (газа) или неподвижное тело обтекается движущейся жидкостью, поэтому в дальнейшем не будем различать эти два случая и назовем их одним общим термином "обтекание тел".

Согласно парадоксу Даламбера: обтекание тела произвольной формы конечных размеров несжимаемой идеальной жидкостью или газом должно происходить в отсутствии силы, действующей на тело со стороны потока этой жидкости или газа.

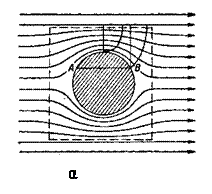При обтекании твердого тела вязкой жидкостью или газом поток деформируется. Слои жидкости, непосредственно соприкасающиеся с телом, прилипают к его поверхности, т. е. вдоль поверхности тела образуется пограничный слой – область, в пределах которой скорость жидкости изменяется от нуля до скорости невозмущенного потока (рис. 1).

В любом сечении потока возникают градиенты скорости. В соответствии со II законом Ньютона в области существования градиентов скорости на тело со стороны потока жидкости или газа действует сила, которую, в общем случае, можно разложить на две составляющие:

,

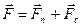где 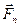- подъемная сила, направленная перпендикулярно данной скорости, 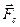- сила лобового сопротивления, взятая в направлении скорости невозмущенного потока (рис. 2) .

Рассмотрим подъемную силу. Течение жидкости или газа может быть двух видов:

1)ламинарное: носит стационарный характер, т. е. скорость частиц среды, проходящих через данную точку пространства, одинакова во времени, поэтому жидкость или газ движутся слоями друг относительно друга;

2)турбулентное (вихревое): течение нестационарно, происходит интенсивное перемешивание слоев.

Английский физик О. Рейнольдс (1842-1912) установил, что характер течения жидкости или газа определяется значением безразмерной величины:

,

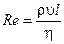которая получила название числа Рейнольдса, где r - плотность жидкости или газа, u - средняя по сечению трубы скорость потока среды, l – характерный для поперечного сечения потока размер, h - вязкость жидкости.

Пока число Рейнольдса мало, всякое возмущение, случайно возникшее в жидкости, гасится, и течение жидкости или газа будет ламинарным. При возрастании ско-рости и размеров потока случайные искривления траекторий движения частиц жидкости или газа воз­никают легче и существуют доль­ше. Этому режиму течения соответствует некоторая об­ласть значений числа Рейнольд­са, которая называется крити­ческой. Наконец, если число Рейнольд­са больше критического значения, случайно возникшие возмущения развива­ются в толще потока, и течение становится турбулентным.

Причиной возникновения подъемной силы является турбулентное течение (циркуляция) жидкости или газа в пограничном слое вокруг тела, обтекаемого потоком. Циркуляция жидкости или газа возникает, например, при обтекании потоком вращающегося кругового цилиндра (эффект Магнуса) или при обтекании тела, несимметричного относительно скорости невозмущенного потока (профиль Жуковского).

В обоих случаях скорость потока над телом больше, чем под телом, следовательно, согласно уравнению Бернулли, давление под телом больше, чем над телом. Возникает разность статических давлений под телом и над телом, что приводит к появлению подъемной силы.

При обтекании симметричного относительно невозмущенного потока тела скорости над телом и под телом равны, поэтому подъемная сила в этом случае равна нулю.

Рассмотрим лобовое сопротивление. В общем случае оно складывается из силы сопротивления трения, связанного с вязкостью жидкости, и сопротивления давления, связанного c разностью давлений на передней и задней относительно невозмущенного потока поверхностях тела.

Скорость в пограничном слое быстро возрастает от нуля, у поверхности тела, до значений близких к скорости невозмущенного потока, что вызывает сильное торможение частиц среды вблизи поверхности тела и ведет к срыву пограничного слоя и вихреобразованию за телом. В потоке, обтекающем тело, образуется зона, заполненная вихрями. Внутри вихрей среда движется быстро, и давление в них меньше давления в окружающей среде. Таким образом, благодаря вихреобразованию, в области за телом давление в среднем понижено по сравнению с давлением в остальных частях среды. Наоборот, перед телом скорость среды уменьшена и поэтому здесь возникает область повышенного давления. Давление около боковых сторон симметричного тела одинаково.

Сила сопротивления давления может быть вычислена по формуле:

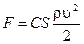, (1)

где ρ – плотность жидкости, S – максимальная площадь поперечного сечения тела, C – безразмерный коэффициент, зависящий от числа Рейнольдса, вязких свойств жидкости и формы тела, u - скорость относительного движения тела.

В таблице 1 приводятся средние значения коэффициентов лобового сопротивления и чисел Рейнольдса для тел различной формы.

Таблица 1.

Форма тела и направление потока	С	Re
Диск		1,11	0 - 5×106
Полусфера		1,35 – 1,40	0 - 5×106
	1,30– 1,40	0 - 5×106
Шар		0,4	2×103 – 2,5×105
0,1 – 0,2	3×105 - 7×106
Удобообтекаемое тело вращения		0,045	1,5×105 - 6×106
	0,1	1,5×105 - 6×106

Так как сила сопротивления давления прямо пропорцианальна квадрату скорости относительного движения тела в жидкости или газе, то при малых скоростях (малых числах Рейнольдса) преобладающим оказывается сила сопротивления трения, при больших – сила сопротивления давления. В широком диапазоне промежуточных скоростей (критических значений чисел Рейнольдса) расчет общего сопротивления движению тела представляет сложную задачу.

В настоящей работе предлагается сравнить между собой лобовые сопротивления тел различной формы и одинакового поперечного сечения при обтекании их воздушным потоком с большими значениями числа Рейнольдса.

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Воздуходувная труба имеет внутри вентилятор, создающий воздушный поток. Чтобы сделать поток более однородным, в трубе установлена сотовая решетка, дробящая крупные вихри на вихри, размеры которых много меньше размеров тела. Воздушный поток выходит из трубы через круглое сопло и направляется на тело. Тело А крепится перед трубой на аэродинамических весах.

Схема аэродинамических весов показана на рис. 3. Основная часть – крестообразное коромысло, которое может совершать колебания около оси О. К нему подвешивается испытуемое тело А. На коромысле закреплены два неподвижных противовеса. Длинное плечо горизонтальной части коромысла снабжено указателем К и шкалой, вдоль которой можно смещать груз Р, изменяя этим плечо а.

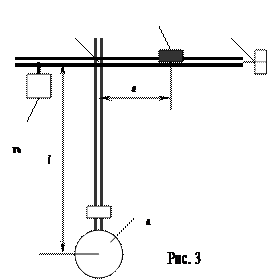На коротком плече горизонтальной части коромысла имеется демпфер D (глушитель колебаний), состоящий из диска, опущенного в масло. Демпфер вызывает быстрое затухание колебаний коромысла, что облегчает отсчет.

Прикрепив к коромыслу испытуемое тело, масштабной линейкой измеряют расстояние от оси до центра испытуемого тела. Затем груз Р передвигают, добиваясь, чтобы указатель К стоял против средней метки на шкале. Пусть левый край груза при этом находится напротив деления а₁. При запуске воздуходувной трубы равновесие коромысла нарушается. Передвигая груз Р, добиваются, чтобы указатель К снова установился напротив средней метки. Пусть это имеет место, когда груз Р находится против деления а₂.

При отсутствии потока воздуха равновесие весов определяется условием:

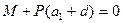, (2)

где М – сумма вращающих моментов, созданных весом всех частей коромысла, кроме груза Р, d – расстояние центра масс груза от его левого края, Р – вес груза.

При наличии потока равновесие определяется условием:

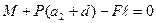. (3)

Из (2) и (3) следует:

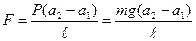, (4)

где m – масса груза Р.

ЗАДАНИЕ

1. На коромысле последовательно укрепить: диск, шар, полушар и удобообтекаемое тело одинакового максимального сечения. Два последних тела ставятся в двух положениях, отличающихся на 180°. Тела устанавливаются на оси сопла в 15-20 см от его внешнего среза так, чтобы их ось симметрии была параллельна оси потока. Измерить значения а₁ и а₂ трижды для каждого тела.

2. Вычислить силу лобового сопротивления для каждого тела. Рассчитать процентное отношение лобового сопротивления данного тела к сопротивлению диска.

РЯДЫ РАСПРЕДЕЛЕНИЯ. СРЕДНИЕ ВЕЛИЧИНЫ. ПОКАЗАТЕЛИ ВАРИАЦИИ И ДРУГИЕ ХАРАКТЕРИСТИКИ РЯДОВ РАСПРЕДЕЛЕНИЯ. СТАТИСТИЧЕСКИЕ ГРАФИКИ