Изображение прямой линии на комплексном чертеже
Проекцией прямой линии как совокупности проекций всех её точек является прямая линия. Следовательно, пространственная прямая определяется на двухкартинном комплексном чертеже парой своих проекций.
В начертательной геометрии различают прямые общего и частного положения. Прямые, наклонённые ко всем плоскостям проекций, называются прямыми общего положения (прямая l на рисунке 1.3.1). Прямые, перпендикулярные либо параллельные плоскости проекций, называются прямыми частного положения (прямые i, q, p’, h, f, p в соответствии с рисунком 1.3.1).
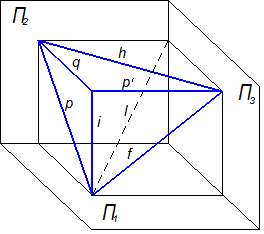
Рисунок 1.3.1 – Положение прямой относительно плоскостей проекций
Прямые частного положения разделяются на проецирующие прямые(перпендикулярные плоскости проекций) и на прямые уровня (параллельные одной плоскости проекций).
Прямая общего положения называется восходящей, если её проекции ориентированы одинаково (прямая l на рисунке 1.3.2), и нисходящей, если её проекции ориентированы противоположно (прямая m на рисунке 1.3.2). У прямой l ближайшая к наблюдателю точка М (наблюдатель предполагается стоящим лицом к плоскости П2) располагается ниже, чем более удалённая от наблюдателя точка N. Эта прямая по мере удаления от наблюдателя поднимается вверх (восходит). Прямая m по мере удаления от наблюдателя понижается (нисходит). Ориентация проекций восходящей прямой l и нисходящей прямой m обозначена стрелками.
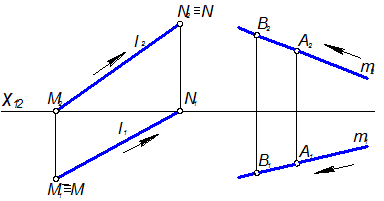 |
Рисунок 1.3.2 – Комплексный чертёж прямых общего положения
Дата добавления: 2015-02-13; просмотров: 1194;
