Основні закономірності пробою твердих діелектриків
Тверда ізоляція є однієї з найпоширеніших . Це пояснюється її високою електричною міцністю, гарними тепловими й механічними характеристиками можливістю використовувати її для сприйняття механічних навантажень.
Розглянемо закономірності пробою твердої ізоляції за загальною схемою: джерела носіїв заряду в слабких полях, процеси збільшення їхньої кількості в сильних, вторинні процеси й критерії пробою.
Як і у випадку газів і рідин для твердих діелектриків з ковалентними зв'язками поява вільних носіїв струму обумовлено іонізацією космічними променями, термогенерацією і наявністю домішок і дефектів структури, що полегшують термогенерацію. Носіями струму є в основному електрони, якщо не враховувати домішкової електропровідності, яка може бути й іонною. В іонних кристалічних діелектриках, на відміну від молекулярних, основний внесок в електропровідність дають іони в міжвузлях або іонні вакансії (діркова електропровідність). Концентрація тих і інших визначається звичайною формулою
n~Nexp(-W/kT)
де n - число атомів в 1 см3;
W - енергія активації.
У сильних полях до зазначених процесів генерації носіїв можна долучити також електростатичну іонізацію в діелектриках з вузькою забороненою зоною, термоелектронну емісію за Френкелем й холодну емісію з електродів.
Провідність твердих діелектриків у сильних полях росте з напруженістю поля у відповідності з формулами Пуля або Френкеля
s=s0exp(Bt) , 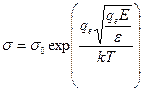
Залежно від переважного процесу збільшення кількості носіїв заряду - ударної іонізації або термогенерації електронів і вільних іонів - розрізняють електричну або теплову форми пробою твердих діелектриків. Обговорювалася гіпотеза про електромеханічний пробій, що полягає в механічному руйнуванні твердих тіл електростатичними силами. Всі інші форми пробою - електрохімічний пробій, іонізаційний і ін. є власне кажучи підготовчими стадіями, процесами старіння, що ослаблюють діелектрик і приводять до його пробою за одним із двох основних механізмів, частіше тепловому.
Як основний процес збільшення кількості носіїв при електричному пробої розглядається ударна іонізація електронами. Теорії електричного пробою твердих діелектриків відрізняються критеріями пробою. Одними з перших були сформульовані критерії Хіппеля й Фрьоліха.
Відповідно до першого – пробій можливий за умови, що кожний вільний електрон, прискорюючись в електричному полі, здобуває енергію, достатню для подолання гальмування граткою в області максимальної взаємодії. Відповідно до другого - пробій відбувається в тому випадку, коли тільки швидкі електрони, що мають енергію, порівнянну з енергією іонізації діелектрика, у стані перебороти гальмування граткою (рис. 34).
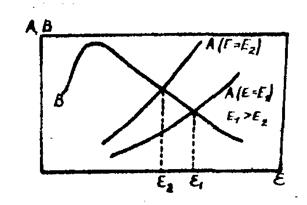
Рис. 34. Залежність енергії, яку здобуває (А) електрон і віддає (В) кристалічній гратці.
Відсутність кореляції між електричною міцністю й енергією іонізації послужило причиною відмови від критерію Фрьоліха. Більш коректний критерій пробою був запропонований Давидовим і Шмушкевичем, згідно якого пробій настає, коли при збільшенні напруженості поля починає з'являтися відхилення функції розподілу електронів від функції розподілу електронів для рівноважного стану, яке проявляється у збільшенні частки швидких електронів. Процеси іонізації починають переважати над процесами рекомбінації. У більше детальному формулюванні В.А. Чуєнкова цей критерій трансформований у вимогу: після іонізації залишкова енергія половини електронів повинна бути достатньою для подолання гальмування граткою, внаслідок чого число швидких електронів повинне наростати з часом.
У теоріях Хіппеля й Фрьоліха енергія, яку здобуває електрон за секунду, приймається рівною
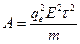
де m, qe - маса й заряд електрона;
E - напруженість поля;
t - час релаксації, за який імпульс електрона зменшується в е раз.
Час релаксації 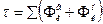 , де
, де 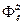 й
й 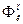 - імовірності випущення до поглинання електроном фонона із хвильовим числом коливань гратки k (k=2p¤l, де l - довжина хвилі коливання).
- імовірності випущення до поглинання електроном фонона із хвильовим числом коливань гратки k (k=2p¤l, де l - довжина хвилі коливання).
Втрати енергії на коливаннях гратки
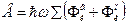 ,
,
де w - частота оптичних коливань гратки ( у теорії Черенкова враховуються і акустичні коливання).
Критерії пробою мають вигляд:
згідно Хіппеля - А=В при 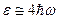 , де e - енергія електрона,
, де e - енергія електрона,
згідно Фрьоліха - А=В при e=І , де І – енергія іонізації (І> 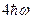 )
)
згідно Чуєнкову - eм=eр, де eм - медіанне значення енергії електронів після іонізації, eр - значення енергії, при якому електрони передають гратці таку ж кількість енергії, що одержують від поля.
Оцінки значень eм і eр мають вигляд:
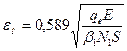 ,
,
де E – напруженість поля, В/см;
b1 - число електронів на зовнішній оболонці;
N1 - число іонів в одиниці об'єму кристала;
S - коефіцієнт пропорційності між ефективним перетином іонізації й різницею (e - І) ,
S~10-6 – 10-5c2/r , eр=a12B(eр)2, a1 - розмірний коефіцієнт (для NaCl a1=15,4×10-10 Дж/с).
Електрична міцність відповідно до теорій Хіппеля й Фрьоліха визначається виразом 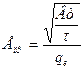 .
.
Так як B 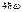 >>BI , а tI >>t
>>BI , а tI >>t 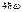 , то обидві теорії, незважаючи на різке розходження критеріїв, дають близькі розрахункові значення.
, то обидві теорії, незважаючи на різке розходження критеріїв, дають близькі розрахункові значення.
Більше детальне врахування зміни ефективного заряду іонів при утворенні твердого тіла, проведений Чуєнковим, показав, що теорія Хіппеля дає завищені в 5-6 разів значення електричної міцності в порівнянні з експериментальними, а теорія Фрьоліха - занижені в кілька разів. Теорія Чуєнкова дає близькі до експериментальних результати для лужно-галоїдних кристалів. Розрахунки для інших матеріалів не можна виконати через відсутність відомостей про характеристики елементарних процесів, що використовуються у теорії.
У всіх розглянутих теоріях розрахунки виконувалися для лужно-галоїдних кристалів у наближенні вільних електронів. Як було показано К.Б. Толпиго, це наближення не коректне, тому що в іонних кристалах електрони перебувають у поляронному стані і їхня маса приблизно на два порядки перевищує ефективну масу електрона, розраховану в рамках зонної теорії. Така велика ефективна маса електрона в поляронному стані пояснюється його поляризуючою дією на гратку. Електрон відштовхує негативні іони й притягає позитивні, утворюючи навколо себе потенційну яму. Для переміщення полярону - електрона разом з викликаним ним збуренням - необхідно витрачати більшу енергію, тому що частина її йде на перебудову гратки. Хоча основи поляронної теорії пробою були розроблені (Ю.І. Гаркуном і К.Б. Толпиго), але вона не була доведена до інженерного рівня.
Ю.М. Вершиніним був даний детальний якісний аналіз явищ електропровідності й пробою з врахуванням не тільки ударної іонізації, яка розглянута у наведених вище теоріях, але й стадії руйнування. Використовуючи критерій А.А. Воробйова
A=B,
де 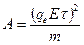 , B=cU
, B=cU
с - коефіцієнт пропорційності;
U - енергія гратки,
і уявлення про пробій, як про процес переродження твердого діелектрика в плазму під дією ударної іонізації електронами й дірками, іонізації фотонами, що утворюються в процесі випромінювальної рекомбінації електронів і дірок, електростатичної іонізації, обумовленої тунельним переходом електронів спочатку на акцепторні рівні, а потім і в зону провідності в електричному полі, що утворилося у результаті прояву нестабільності концентрації носіїв в області об’ємного заряду, нагрівання гратки діелектрика при не випромінюючих процесах гальмування й рекомбінації, нагрівання діелектрика джоулевою теплотою, Вершинін обґрунтував вид емпіричної формули для розрахунку імпульсної електричної міцності твердих діелектриків
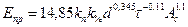
де kn - коефіцієнт, що враховує форму поля й полярність імпульсу (для електродів вістря-площина kn = 1 при позитивному й 1,52 - при негативному вістрі, для електродів куля - площина kn = 1,82);
k%= 1- коефіцієнт, що враховував імовірність пробою;
d- товщина діелектрика, ;
t- тривалість імпульсу, мкс;
Ac - питома енергетична характеристика діелектрика, що вираховується за формулою
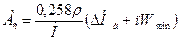 , кДж/см
, кДж/см
де r - щільність діелектрика, г/см3;
М - молекулярна маса;
DНа- сумарна енергія зв'язку, кДж/моль;
n- число атомів, що мають мінімальну енергію іонізації .
Величина Ас містить енергію ґраток (для кристалів), енергію сублімації й енергію дисоціації в залежності від будови діелектрика. У випадку полімерів DНа=SтіDi, де mі - число зв'язків з енергією дисоціації зв'язку Di. Формули Ю.Н. Вершиніна дають результати, близькі до експериментальних.
З короткого огляду найбільш поширених теорій електричного пробою твердих діелектриків видно, що всі вони мають один недолік – невизначеність критерію пробою. Якщо підходити до пробою як нестаціонарного явища, то необхідно виділити основні вторинні процеси, які могли б забезпечити спадну вольт-амперну характеристику, забезпечуючи зворотний позитивний зв'язок. Роль вторинних процесів грають, цілком ймовірно , ударна іонізація носіями протилежного знака й вторинна холодна емісія з катода.
Теорія теплового пробою твердих діелектриків розвинута Фоком, Вальтером і Семеновим набагато досконаліше. Основним вторинним процесом, відповідно до цієї теорії, є ріст провідності або tgd при нагріванні, який відображається експонентами: 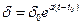 і
і 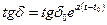 де d й tgd визначають енергію, що виділяється у твердому діелектрику, при постійній і змінній напрузі відповідно. Ця енергія шляхом теплопровідності відводиться від діелектрика до електродів, а від них у навколишній простір. Відповідно до закону Ньютона кількість відведеної теплоти прямо пропорційна різниці температур, у той час як енергія, що виділяється в діелектрику під дією поля, експоненціально зростає. При певній напруженості теплота не встигає відводитися й відбувається саморозігрівання діелектрика, що кінчається пробоєм (рис. 35).
де d й tgd визначають енергію, що виділяється у твердому діелектрику, при постійній і змінній напрузі відповідно. Ця енергія шляхом теплопровідності відводиться від діелектрика до електродів, а від них у навколишній простір. Відповідно до закону Ньютона кількість відведеної теплоти прямо пропорційна різниці температур, у той час як енергія, що виділяється в діелектрику під дією поля, експоненціально зростає. При певній напруженості теплота не встигає відводитися й відбувається саморозігрівання діелектрика, що кінчається пробоєм (рис. 35).
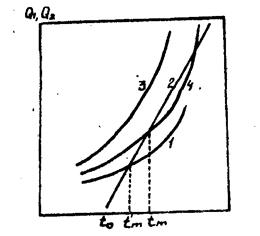
Рис. 35. Залежність тепловиділення (1,3,4) і тепловіддачі (2) від температури.
Розв’язок диференціального рівняння, що описує тепловий баланс у діелектрику, дає з умови його порушення для плоского зразка
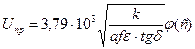 ,
,
де k- коефіцієнт теплопровідності діелектрика;
φ(c) - функція від 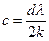 ,
,
де d - товщина ізоляції;
l - коефіцієнт теплопровідності області між діелектриком і електродами.
Ця функція має вигляд, показаний на рис. 35 (крива?)
Для циліндричних зразків
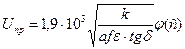 ,
, 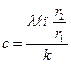
Теорія Фока-Вальтера-Семенова широко застосовується для технічних розрахунків високовольтної ізоляції.
Відзначимо основні закономірності теплового пробою. Unр істотно залежить від температури навколишнього середовища, що визначає значення tgd, що входить у формулу для Unр. Звичайно значення беруть при 20°С. Його величина може служити критерієм стійкості діелектрика до теплового пробою. Як відомо, на низьких частотах на величину tgd помітно впливають зволоження й абсорбційні процеси. Тому зволожена й неоднорідна ізоляція менш надійна. Враховуючи, що tgd при сильному зволоженні, великій неоднорідності й наявності релаксаційних процесів залежить від частоти, при розрахунках необхідно брати його значення, що відповідає частоті робочої напруги.
При зміні температури навколишнього середовища застосовується початкове значення tgd, яке відповідає новій температурі, і відповідно змінюється Uпр. Однак, аналогічна залежність від температури спостерігається й при електричному пробої у високотемпературній області за Фрьоліхом. Тому зниження Unр з ростом температури не є характерною ознакою теплового пробою. Звичайно тепловий пробій характеризується залежністю Unр від частоти й форми випробувальної напруги й умов відведення теплоти. Крім того, тепловий пробій відрізняється великою інерцією. Встановлення рівноважного стану і його порушення можуть тривати хвилинами, а іноді й годинами, на відміну від електричного пробою, де час формування пробою обчислюється частками секунди. При тепловому пробої спостерігається нелінійність Unр(d). Розвиток теплового пробою при постійній напрузі звичайно пов’язують з нестабільністю іонної провідності діелектрика. У більшості ковалентних і молекулярних бездомішкових діелектриків, тому, повинен мати місце електричний пробій.
Однак, як було встановлено В.Д. Кучіним, при дуже коротких імпульсах, Unр для лужно-галоїдних кристалів перестає залежати від температури, що суперечить обом теоріям. Крім того, Старком і Гертоном була встановлена аналогія в зміні модуля Юнга й Unр опроміненого поліетилену (рис. 36)
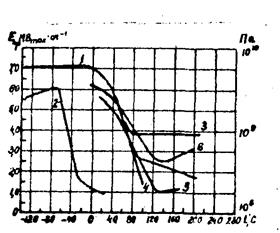
Рис. 36. Залежність електричної й механічної міцності від температури.
Це дозволило сформулювати гіпотезу про електромеханічний пробій. При дуже коротких імпульсах напруги діелектрик випробовує ударне навантаження, що може перевищити його механічну міцність. Для полімерів, що мають порівняно малий модуль Юнга, при електростатичному стиску матеріалу деформація може досягти такої величини, що зразок стане механічно нестійким. В області високих температур при зазначених припущеннях можна дістати кількісне узгодження з експериментом.
Пробивна напруга твердих діелектриків звичайно розраховується за формулою
Unp=Enpd
Причому Enp береться з довідників електроізоляційних матеріалів. Однак, при цьому варто враховувати, що Unp твердої ізоляції, як і газової, і рідкої, залежить від конфігурації електродів, стану й структури матеріалу й форми напруги, що впливає на матеріал.
Наприклад, міцність литої епоксидної ізоляції в системі електродів різної конфігурації залежить від товщини як наведено на рис. 37:
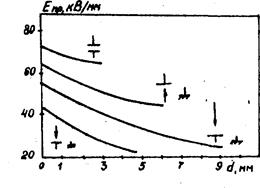
Рис. 37. Залежність електричної міцності епоксидних компаундів
від товщини діелектриків у неоднорідному полі.
Як і у випадку газів і рідин мінімальна Unp має місце для проміжку вістря-площина при позитивній полярності вістря. Крім того, у різко нерівномірному полі порушується пропорційність між Unp і d (рис. 38)
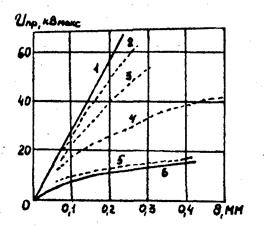
Рис. 38. Залежність пробивної напруги скла від відстані між платиновим
дротом діаметром 1 мм (2), 0,3 мм (3), 0,1 мм (4), 0,03 мм (5) і площиною.
1 - однорідне поле; 6 - мінімальні значення.
Аналогічні залежності спостерігаються й для інших твердих діелектриків. Причому чим більше їхня неоднорідність, тим більше виражена залежність Unp від d і рівномірності поля. Так, наприклад, Unp порцеляни різко знижується зі збільшенням довжини пор на 1 мм зразка (рис. 39).
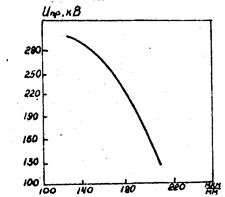
Рис. 39. Залежність пробивної напруги порцеляни від довжини пор.
Залежність Unp від форми напруги, що впливає на матеріал, уже частково обговорювалася. При тепловому пробої Unp~f -0.5. При електричному Unp не залежить від частоти, однак, як і при пробої газів і рідин, у випадку дуже коротких імпульсів спостерігається збільшення Unp, обумовлене статистичним характером пробою (рис. 40). Для неоднорідних діелектриків в області більшої тривалості дії напруги спостерігається ще одна область зниження електричної міцності внаслідок впливу дефектів, просторових зарядів, розігрівання й т.п.
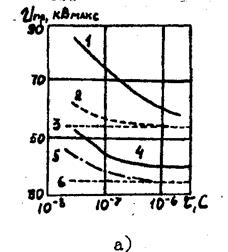
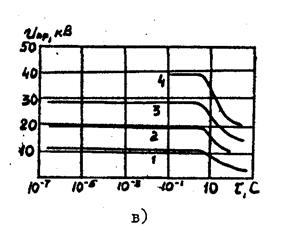
Рис. 40. Залежність пробивної напруги скла від тривалості імпульсу
в неоднорідних (а) і однорідних (в) полях.
Збільшення тиску звичайно слабко впливає на пробій твердих діелектриків. Спостерігається незначне його підвищення, обумовлене збільшенням густини діелектрика.
Тепловий пробій відбувається у тому випадку, коли порушується рівновага між кількістю теплоти, що виділяється в діелектрику, і відведеною у зовнішнє середовище. За пробивну напругу при тепловому пробої приймають мінімальну напругу, при якій відбувається порушення теплової рівноваги.
При тепловому пробої плоского діелектрика пробивна напруга дорівнює
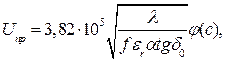
де er, tgd0 - характеристики діелектрика при температурі навколишнього середовища;
a - стала, що характеризує зростання tgd з ростом температури;
c - параметр, що характеризує умови відведення теплоти від діелектрика у зовнішнє середовище.
Прийнято, що tgd зростає з температурою за експоненціальним законом:
tgd (T2) = tgd (Т1) exp[a(Т2 –T1)].
При розв'язуванні контрольних задач значення er задається за умовою задачі і вважається сталим. Cталу a можна визначити так:
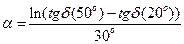 .
.
Таблиця 2
Значення функції φ(с)
| с | φ(с) | с | φ(с) | с | φ(с) |
| 0,010 | 0,040 | 0,09 | 0,123 | 1,0 | 0,37 |
| 0,015 | 0,050 | 0,10 | 0,130 | 1,5 | 0,43 |
| 0,020 | 0,065 | 0,15 | 0,160 | 2,0 | 0,46 |
| 0,055 | 0,100 | 0,20 | 0,180 | 4,0 | 0,54 |
| 0,060 | 0,103 | 0,40 | 0,260 | 4,5 | 0,55 |
| 0,070 | 0,110 | 0,60 | 0,300 | 5,0 | 0,56 |
| 0,080 | 0,118 | 0,90 | 0,360 | 9,0 | 0,60 |
Для плоских зразків
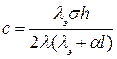 ,
,
де l - теплопровідність електродів, для міді lэ = 0,0109 Вт/м;
σ - коефіцієнт тепловіддачі теплоти у зовнішнє середовище, для повітря σ = ІЗ Вт/м ;
l - товщина електродів (при визначенні параметра c можна вважати електроди надзвичайно тонкими, тобто брати l =0).
Значення φ(c) беруть з табл. 2. Для обчислення проміжних значень c рекомендується застосовувати лінійну інтерполяцію.
Іонізаційний пробій - це пробій, зумовлений іонізаційними процесами внаслідок часткових розрядів у газових порожнинах діелектриків. Враховуючи, що пробій під впливом часткових розрядів значною мірою визначає надійність високовольтного електроустаткування з полімерною ізоляцією, зупинимося на цьому більш докладно.
За означенням до часткових розрядів належать розряди, які не замикають основні електроди каналом високої провідності (корона, розряди у газових порожнинах тощо). Хоча часткові розряди мають малу потужність (енергія приблизно 10-6 Дж, тривалість 10-9... 10-6 с), вони викликають деструкцію і ерозію полімерних діелектриків у місці контакту з каналом розряду та утворення порожнистих розгалужених каналів в об’ємі діелектрика, іноді з провідними стінками. Цей процес називається тріінгом. Основними характеристиками, що використовують для оцінки інтенсивності часткових розрядів, є уявний заряд, частота з’явлення, середній струм. Для об'єктів одного типу час до пробою обернено пропорційний середньому струму часткових розрядів, а уявний заряд зростає з ростом розмірів порожнин. Ці закономірності використовуються для діагностики електричної ізоляції.
Час до пробою ізоляції при дії часткових розрядів є функцією напруженості поля:
τ = B(E - Eвчр)-m,
де В - константа для даного типу діелектрика),
Дану залежність ще називають "кривою життя".
Через те, що часткові розряди супроводжуються зростанням tgd стан ізоляції часто оцінюється також за іонізаційною кривою, яка відображає залежність tgd від напруги. Чим більше дефектів ізоляції, тим раніше спостерігається перегин залежності tgd (U) і тим стрімкіше піднімається крива з ростом напруги.
До іонізаційного пробою дуже подібний пробій полімерних діелектриків у результаті утворення і проростання заповненого водою розгалуженого каналу (водний тріінг), який спостерігається при експлуатації полімерної ізоляції у вологому середовищі, особливо у морській воді або в розчинах електролітів. Зазначимо, що водний тріінг розвивається за змінної напруги. Механізм його розвитку остаточно не встановлений. Однією з причин водного тріінгу може бути електроосмос.
Дата добавления: 2015-02-10; просмотров: 1858;
