Природа і руйнуюча дія часткових розрядів

Ми розглянули механізм протікання часткових розрядів для випадку, коли вони дискретні. Однак деякі дослідники вважають, що часткові розряди можуть протікати за квазістаціонарним механізмом, при якому напруга на порожнині після пробою не змінюється протягом півперіоду. Такі уявлення ґрунтуються на залежності ємності ізоляції із порожниною від напруги, що має вигляд, наведений на рис. 59, і пояснюється закорочуванням ємності порожнини С1 розрядом. Проте дослідження й виміри амплітудно-частотних спектрів часткових розрядів показують, що струм часткових розрядів у широкому діапазоні розмірів порожнин (25 мкм < h < 1200 мкм) імпульсний, а частотний спектр часткових розрядів досягає частот 400 МГЦ, що відповідає тривалості окремих розрядів порядку наносекунд. Ці результати свідчать про дискретний характер часткових розрядів. Збільшення ємності при вимірюванні мостовим методом можна пояснити у випадку дискретних часткових розрядів тим, що адсорбовані на торцях порожнини заряди, індукують на електродах додатковий заряд. У зовнішній схемі цей процес сприймається як збільшення ємності ізоляції, що обумовлене поляризацією порожнини. З огляду на наведені результати, можна вважати, що часткові розряди являють собою імпульсні розряди тривалістю від 10^-9 до 10^-6 с.

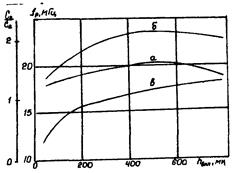
Рис. 59. Залежність ємності діелектрика (a,б) і резонансної частоти контуру (в)

від напруги при наявності часткових розрядів.

Однак, імпульсні розряди можуть бути або лавинними або іскровими із властивими для них розподілом поля, температурою й т.п., а тому по-різному можуть впливати на ізоляцію. Ситуація у випадку часткових розрядів ускладнюється тим, що тривалість їх відповідає іскровим розрядам, а область значень pd - області існування лавинного розряду принаймні до h₁~ 300 мкм. Іскровий розряд можливий лише при h > 1,4 мм при атмосферному тиску. Якщо у випадку металевих електродів малі часи формування лавинних розрядів пояснювалися із залученням в ролі вторинного процесу фотоемісії електронів з катода, то для діелектриків фотоемісія не може грати істотної ролі через відсутність вільних електронів. Наявність же в розряді великої кількості квантів з великою енергією, що могли б вибивати електрони з валентної зони, мало ймовірно. В роботах В.М. Кириленка показано, що якщо враховувати вторинну іонно-електронну емісію, обумовлену розрідженою хмарою позитивних іонів, які залишаються першою лавиною в розрядному проміжку, то для часу формування розрядного каналу можна одержати вираз:

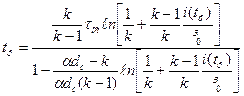
де 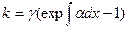- коефіцієнт іонізаційного наростання;

d_c - проміжний перетин розрядного каналу, у якому струм лавини досягає значення i(t_ф), при якому вступають у дію просторові заряди;

і₀- початковий фотострум.

При k >> І

,

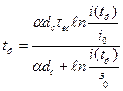а якщо до того ж lni(t_ф)/i₀>>ad_c,то t_ф=ad_ct_ec , чому сприяють підвищені значення g.

Звідси випливає, що при досить великих перенапругах час формування лавинного розряду й без врахування фотоемісії може бути порівняним з часом прольоту електронів. Отже, часткові розряди з повною підставою можна віднести до розрядів, що формуються за лавинним механізмом. Для таких розрядів характерні високі значення напруженості поля в розрядному каналі, що сильно залежать від густини розрядного струму, а порівняно низька температура газу в розрядному каналі – має істотне значення для оцінки їхньої руйнуючої дії на ізоляцію.

Розподіл поля в каналі лавинного розряду описується теорією Роговского. Однак, прийняте в ній співвідношення для щільності електронного струму

, ,????

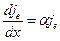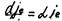де 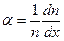- коефіцієнт ударної іонізації,

справедливо тільки для однорідного поля, коли швидкість електронів v постійна за довжиною проміжку. При збільшенні густини струму розподіл поля стає нерівномірним і варто застосовувати співвідношення

.

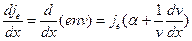З урахуванням цього співвідношення з рівняння Пуассона

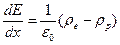
де r_e й r_p - щільності електронів і позитивних іонів відповідно, при 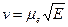, 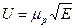можна одержати нелінійне диференціальне рівняння другого порядку, яке описує розподіл поля в лавинному розряді:

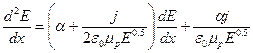
При цьому варто врахувати, що 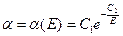. Розв’язати це рівняння в загальному виді не вдається. Частковий розв’язок його має вигляд:

.

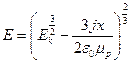(розшифровка)

У перетвореному виді воно дає зв'язок між струмом, напруженістю поля біля катода й величиною катодного падіння, і співпадає з виведеної Энгелем і Літтлем іншим шляхом формулою для густини струму нормального тліючого розряду.

Застосовність отриманого виразу для опису розподілу поля в каналі часткового розряду можна оцінити за величиною густини струму. Густину струму при частковому розряді оцінити експериментально дуже важко, тому доводиться використовувати теоретичні оцінки її величини. Основні труднощі при розгляді часткового розряду як розряду ємності порожнини через опір розрядного каналу полягають в тім, що опір каналу є функцією розрядного струму. Аналогічні задачі розглянуті Драбкіною, Брагінським і ін. для потужнострумових іскрових розрядів, для яких питома провідність d через повну іонізацію газу в розрядному каналі постійна й опір каналу визначається тільки його перетином. Хоча в частковому розряді ступінь іонізації газу нижча й механізм її інший, питому провідність також можна вважати постійною, тому що відношення Е/р , яким вона визначається при ударній іонізації, протягом визначального проміжку часу змінюється слабко. З урахуванням цієї обставини густина струму часткового розряду може бути визначена при розв’язанні системи, що складається з рівнянь балансу енергії розрядного ланцюга

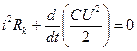
і розрядного каналу

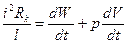
з урахуванням співвідношень

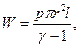p=k₁r₀t²,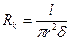

де C = C1, ?

R_k - опір розрядного каналу;

W- внутрішня енергія розрядного каналу;

g - показник адіабати;

l - довжина розрядного проміжку?;

r - радіус розрядного каналу.

Розв’язавши систему рівнянь для густини струму, знаходимо

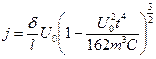
де .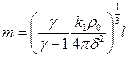

Розрахунок за цією формулою показує, що густина струму часткового розряду може перевищувати густину струму в тліючому розряді. Отже, у ньому може сформуватися до кінця розряду катодна область із підвищеною напруженістю поля. Однак, для формування об'ємного заряду в катода необхідний час порядку 10^-7 с. Часткові розряди, за звичай, тривають десятки наносекунд. Тому не виключено, що розряд гасне перш, ніж приймає форму тліючого розряду.

Гідродинамічна теорія поряд з визначенням густини розрядного струму, дозволяє знайти температуру, обсяг, тиск і інші характеристики розрядного каналу. Це дозволяє оцінити, що є основним руйнуючим фактором при впливі часткових розрядів на ізоляцію.

Найбільш істотними статтями витрати енергії часткових розрядів є резонансне й нерезонансне випромінювання, втрати на іонізацію й на розширення розрядного каналу, накопичування її у вигляді внутрішньої енергії каналу, передача діелектрику при бомбардуванні його поверхні.

На іонізацію витрачається кілька відсотків загальної енергії розряду, а втратами на нерезонансне випромінювання (закон Стефана –Больцмана) можна знехтувати через низьку температуру розрядного каналу (800 - 1000 °С). Робота з розширення розрядного каналу становить близько 28% всієї енергії. / / Для деяких газів, зокрема азоту, істотну частку енергії (до 25%) може нести резонансне випромінювання. Частина енергії, що залишилася (близько 40-65%) передається діелектрику при бомбардуванні його поверхні зарядженими частинками. Слід зазначити, що основну роль будуть грати саме окремі зіткнення, а не розігрівання діелектрика теплопередачею, яке для одиничного розряду становить десяті частки градуса.

Аналіз балансу енергії часткових розрядів показує, що основну роль у руйнуванні ізоляції повинно грати електронно-іонне бомбардування. Цей висновок підтверджується експериментами на моделях ізоляції із порожнинами циліндричної форми, для яких можливий теоретичний розрахунок характеристик інтенсивності часткових розрядів. З врахуванням записаних раніше залежностей для n, Q_x і U_в для моделей із циліндричними порожнинами можна одержати

, ,

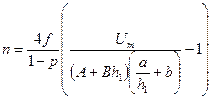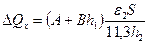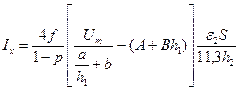
де S - поверхня, що охоплюється розрядом.

Із наведених формул випливає, що, змінюючи товщину порожнини, можна змінювати інтенсивність часткових розрядів при незмінній прикладеній напрузі. Залежність часу до пробою моделей? від товщини порожнини найбільше близько збігається із залежністю середнього струму часткових розрядів від цієї величини (рис. 60).

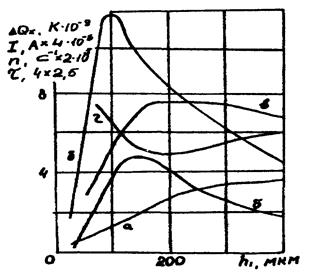
Рис. 60. Залежність уявного заряду (а), частоти проходження (б), середнього струму (в) часткових розрядів і часу безвідмовної роботи (г) від товщини включення.

Якщо врахувати, що час до пробою приблизно становить обернено пропорційну величину середньому струму часткових розрядів, то можна зробити висновок, що він визначається загальною кількістю частинок, що бомбардують діелектрик, а не числом розрядів чи амплітудою окремих розрядів. Цей висновок перебуває в повній відповідності з висновком про вирішальну роль електронно-іонного бомбардування в руйнуванні полімерних діелектриків частковими розрядами.