Часткові розряди у високовольтній ізоляції

Успіхи органічної хімії в створенні полімерних діелектричних матеріалів з високими електрофізичними характеристиками супроводжуються все ширшим впровадженням цих матеріалів в електротехніку. У процесі експлуатації високовольтної полімерної ізоляції було встановлено, що найбільш істотну роль в обмеженні часу до її пробою відіграє руйнуюча дія часткових розрядів.

Частковими розрядами називають розряди, при яких один або обидва електроди ізольовані від розрядного каналу шаром газоподібного, твердого або рідкого діелектрика. Тобто при частковому розряді основні електроди не закорочуються каналом високої провідності.

У газоподібних діелектриках часткові розряди можливі у вигляді коронного розряду в різко нерівномірному?(неоднорідному) полі. Під його дією може спостерігатися утворення хімічно активних продуктів у газі, які потім шкідливо впливають на ізоляцію або струмоведучі елементи. У добре вакуумованій рідинній або просоченій ізоляції часткові розряди, починаючись у найбільш напружених місцях, викликають розкладання рідинного діелектрика. У результаті утворюється газ, що збирається в бульбашки, у яких потім у свою чергу виникають інтенсивні критичні часткові розряди, тому що електрична міцність газу значно нижче міцності рідини. Під дією цих розрядів ізоляція пробивається за короткий час. Час до пробою рідинної й просоченої ізоляції визначається розчинністю газів, що утворяться при впливі початкових часткових розрядів.

У твердих діелектриках часткові розряди виникають у повітряних або газових порожнинах, які неминуче утворюються в процесі виготовлення або експлуатації. У цьому випадку інтенсивність часткових розрядів майже постійна аж до пробою ізоляції. Зниження часу до пробою ізоляції при наявності часткових розрядів характерно для всіх твердих діелектриків, але особливо істотно для полімерів. Маючи малі ε =2 - 5 і tgd = 10^-4 -10^-3, велику електричною міцністю (1 МВ/см), полімерні діелектрики під час відсутності часткових розрядів могли б працювати при більших електричних навантаженнях тривалий час. Часткові розряди скорочують його в сотні й тисячі разів, обмежуючи тим самим можливості органічної ізоляції. З огляду на важливість проблеми підвищення терміну служби полімерної ізоляції, розглянемо її більш докладно.

Часткові розряди починаються за умови, що спадання напруги на порожнині дорівнює пробивному напрузі газу у ній. Напруга виникнення часткових розрядів, тобто прикладена до ізоляції напруга, при якій починаються часткові розряди, неоднакова на постійному й змінному струмах, тому що постійна напруга розподіляється за провідностями, а змінна - за діелектричними проникностями. Для розгляду умов виникнення часткових розрядів звичайно користуються еквівалентною схемою діелектрика із порожниною (рис. 53).

.

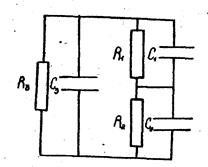
C1, R1 – для порожнин, C2, R2 і C3, R3 – для діелектрика

Рис. 53. Еквівалентна схема діелектрика із порожнинами:

Для визначення напруги виникнення розрядів достатньо розглянути розподіл напруги за ланцюжком C1, R1 C2, R2, зневажаючи шунтувальною дією C3 і R3. На практиці завжди виконуються умови

R1 >> R2 , t₁>>t₂

де t - стала часу.

При постійній напрузі еквівалентна схема діелектрика із порожниною трансформується в послідовне з'єднання опору твердого діелектрика R2 і ємності порожнини С1. При під’єднанні діелектрика із порожниною до джерела постійної напруги при t=0, напруга спочатку розподілиться за ємностями, тобто

,

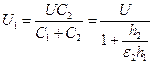де h–?

Якщо U₁ = U_np, то відбудеться перший розряд, напруга на порожнині в результаті заряду поверхні порожнини знизиться до напруги гасіння розряду й розряд припиниться. Якщо проводити експеримент на моделях з відомими e й h, то можна встановити, що U_np газу у порожнині приблизно така ж або на 10-20% нижча ніж для газу між металевими електродами аналогічної конфігурації. Напруга гасіння розряду найчастіше приймається рівною нулю (хоча існують думки, що воно становить близько 80% , а то й до 100%).

Після розряду почнеться релаксація об'ємних зарядів, що осіли на поверхні порожнини й поступове зростання напруги на ній від нуля. Швидкість наростання визначається сталою часу t = R₂C₁. Для реальних діелектриків вона становить одиниці - сотні секунд. Тому при постійній напрузі часткові розряди відбуваються дуже рідко. Частоту їхнього проходження можна визначити з умови U₁ = U_np. Ґрунтуючись на еквівалентній схемі діелектрика із порожниною, маємо

U₁ = U_np(1 – e^-t/t),

де U_о - величина прикладеної постійної напруги .

При розряді U₁ = U_np=U₀(1 – e^-t/t). Звідси для часу між двома розрядами t_p, знаходимо .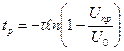

Залежно від U₀ величина ? може бути більше або менше t. t_p= t при U₀ = 1,58 U_np. Загальний характер залежності напруги на порожнині від часу наведений на рис. 54, а залежності t_p від Е на рис. 55.

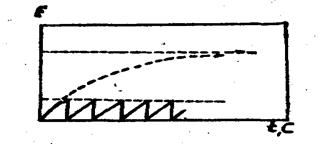
Рис. 54. Схема часткових розрядів при постійній напрузі.

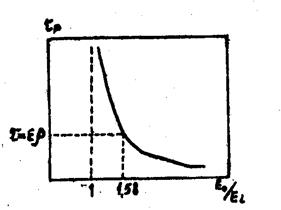
Рис. 55. Залежність часу між розрядами від напруженості поля.

Частота проходження розрядів при постійній напрузі дорівнює

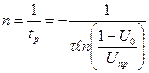
Звичайно число розрядів значно перевищує розрахункове. Це пов'язане зі швидким відновленням напруги на порожнині після закінчення розряду до (0, 8 - 0,9)U_пр. Найбільш імовірною причиною відновлення є рекомбінація об'ємного заряду розрядного каналу, хоча не виключена й підзарядка порожнини за рахунок прилягаючих областей діелектрика.

Частота проходження є однієї з характеристик інтенсивності часткових розрядів. Іншими найбільш вживаними характеристиками інтенсивності часткових розрядів є уявний заряд DQ_x і відносна інтенсивність або середній струм часткових розрядів I_x.

Уявний заряд - це міра найбільшого заряду, що компенсується у зразку при одиничному частковому розряді. Справа в тому, що кожний розряд супроводжується швидкою нейтралізацією накопиченого на порожнині заряду U_npC₁. Така нейтралізація еквівалентна подачі на порожнину східчастої напруги - U_np. Враховуючи, що розряд проходить дуже швидко, впливом опорів можна знехтувати й розглядати чисто ємнісну еквівалентну схему діелектрика із порожниною. З неї випливає, що нейтралізація заряду на порожнині приведе до зниження напруги на C3 (або на електродах) на величину 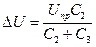. При цьому в зовнішньому ланцюзі це зниження буде сприйматися як втрата зразком частини заряду 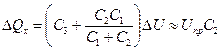,тому що звичайно C₃>>C₁ й C₂ .

Середній струм часткових розрядів дорівнює заряду, що діє у зразку за 1 с, тобто I_x=n×DQ_x.

При змінній напрузі впливом опорів на розподіл напруги також можна знехтувати. Тоді згідно трьохємнісній еквівалентній схемі для моделі ізоляції із порожниною циліндричної форми з умови U_1m=U_np для максимального значення напруги виникнення маємо

.

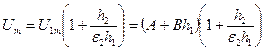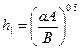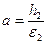При 50 мкм £ h₁ £ 600 мкм А= 0.5 кВ, В= 44 кВ/см. Напруга початку часткових розрядів монотонно зростає зі збільшенням товщини діелектричного шару h₂, розташованого послідовно із порожниною (рис. 56) і проходить через мінімум при , де , причому 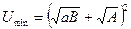(рис. 57).

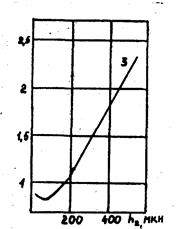
Рис. 56. Залежність напруги виникнення часткових розрядів від товщини діелектрика.

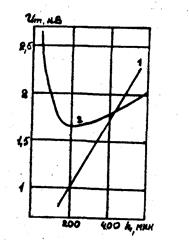
Рис. 57. Залежність напруги виникнення часткових розрядів від товщини порожнини при постійній (1) і змінній (2) товщині діелектрика.

Сам процес часткових розрядів протікає при змінній напрузі в такий спосіб (рис. 58).

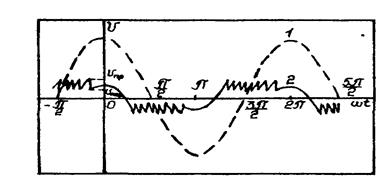
Рис. 58. Зміна напруги на порожнині при часткових розрядах.

Спочатку напруга на порожнині змінюється, як і прикладена за синусоїдальним законом, доки U не стане рівним U_np. При U = U_np відбудеться пробій порожнини. Наскрізна провідність діелектрика дуже мала в порівнянні із провідністю плазми розряду, тому в процесі розряду спливе? поляризація іонізованого газу. У результаті поле в розрядному каналі, що дорівнює сумі полів джерела й об'ємного, заряду стане близьким до нуля. Розряд згасне. Після гасіння розряду концентрація заряджених часток у розрядному каналі почне зменшуватись відповідно до співвідношення

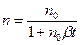
де n₀ - початкова концентрація;

b – коефіцієнт рекомбінації.

При n₀~10¹⁴cм³ і b=10^-6см³/с концентрація зменшиться вдвічі за 10^-8 с. Таким чином, електрична міцність проміжку швидко відновлюється.

Через рекомбінацію об'ємного заряду напруга на порожнині відновлюється від U₂@0 до 0.7 - 0.9 U_np. Після рекомбінації поле у порожнині визначається полем джерела й полем адсорбованих зарядів, що становить (0,3 - 0,1) Е_пр. Тому при подальшому підвищенні прикладеної напруги, напруга на порожнині змінюється еквідистантно? тій синусоїді, що мала б місце, якби розряд був відсутній, проходячи нижче її на постійну величину U_np. Як тільки напруга U? стане знову рівною U_np , відбудеться новий розряд і все повториться спочатку.

Для числа розрядів за півперіод на підставі рис. 58 можна записати вираз

.???

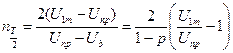
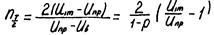Тоді для частоти проходження (чого?) за секунду маємо

???

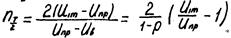а з врахуванням того, що 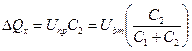для середнього струму часткових розрядів можна записати

.

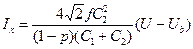При кожному розряді у порожнині виділяється енергія, що дорівнює 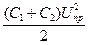. Тому виникнення часткових розрядів супроводжується зростанням втрат потужності. Потужність, що втрачається при часткових розрядах дорівнює

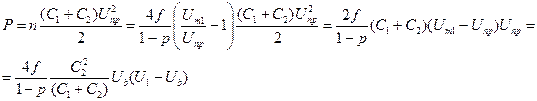
Реактивна потужність ~U², тому при часткових розрядах кут втрат tgd ~ U_b(U-U_b)/U², тобто має максимум залежно від напруги при U=2Uв?. Якщо в ізоляції є багато порожнин різних розмірів, то всі характеристики інтенсивності (чого?) більш складним чином залежать від напруги. Зокрема DQ_x – зростає, а n і І_x стають нелінійними функціями напруги, U_в, і tgd розмиваються (стають незначними)?.