Особенности и физическая реализуемость звеньев

Пусть звено имеет передаточную функцию .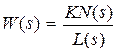

Если нули передаточной функции (корни уравнения N(s) = 0)и полюса передаточной функции (корни уравнения L(s) = 0) имеют действительные части, отрицательные или равные нулю, то такое звено будем называть звеном минимально-фазового типа. При наличии хотя бы одного нуля или полюса с положительной вещественной частью звено будет относиться к нeминимально-фазовому типу.

Рассмотрим эти звенья на простейшем примере. Для звена с передаточной функцией 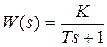, которое является минимально-фазовым, 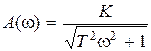, 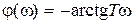. Звено с передаточной функцией 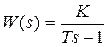, являющееся неминимально-фазовым, имеет частотные характеристики , .

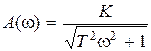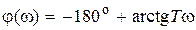Таким образом, при одинаковых АЧХ неминимально-фазовое звено имеет больший по модулю фазовый сдвиг.

Указанное свойство справедливо и в общем случае.

Рассмотрим еще одно важное свойство звеньев – свойство физической реализуемости.

Для любого реального устройства АЧХ с увеличением частоты должна уменьшаться и стремиться к нулю, а фазовые сдвиги на высоких частотах должны быть отрицательными. Пусть полином числителя КN(s) передаточной функции W(s) имеет порядок m, а полином знаменателя 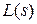– порядок 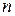. Тогда для минимально-фазового звена справедливы следующие соотношения:

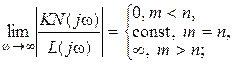
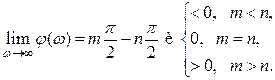
Из приведенных соотношений следует, что звено является физически реализуемым, если будет выполняться соотношение .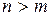

С этой точки зрения, например, идеальное дифференцирующее звено с передаточной функцией W(s) = Ks не является физически реализуемым. Реальное звено, осуществляющее операции дифференцирования, может быть аппроксимировано передаточной функцией W(s) = Ks в некотором ограниченном диапазоне частот.