Частотные характеристики систем
Частотные методы анализа и синтеза систем управления находят широкое применение в инженерной практике. По аналогии с частотными характеристиками звеньев можно ввести соответствующие частотные характеристики для системы автоматического управления.
Важным классом частотных характеристик являются частотные характеристики разомкнутой системы, определяемые из передаточной функции W(s). Это амплитудно-фазовая частотная характеристика 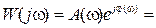
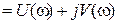 ,где
,где 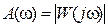 – АЧХ;
– АЧХ; 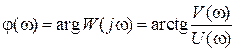 – ФЧХ;
– ФЧХ; 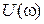 ,
, 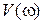 – соответственно вещественная и мнимая частотные характеристики,
– соответственно вещественная и мнимая частотные характеристики, 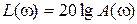 – логарифмическая амплитудная частотная характеристика разомкнутой системы.
– логарифмическая амплитудная частотная характеристика разомкнутой системы.
Отметим некоторые общие свойства частотных характеристик для систем минимально-фазового типа. Пусть 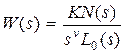 и степень полинома числителя m меньше степени полинома знаменателя n, тогда
и степень полинома числителя m меньше степени полинома знаменателя n, тогда
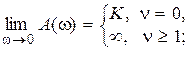
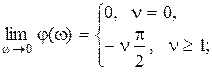
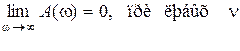 ;
; 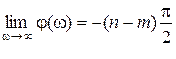 .
.
При этом годограф 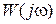 на комплексной плоскости при
на комплексной плоскости при 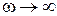 стремится к началу координат, при
стремится к началу координат, при 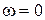 для статической системы он начинается на действительной оси на расстоянии K от начала координат, а для астатических систем при
для статической системы он начинается на действительной оси на расстоянии K от начала координат, а для астатических систем при 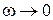 уходит в бесконечность в третьем квадранте при
уходит в бесконечность в третьем квадранте при 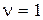 , во втором квадранте при
, во втором квадранте при 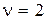 , в первом квадранте при
, в первом квадранте при 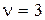 и т.д. по часовой стрелке.
и т.д. по часовой стрелке.
При построении частотных характеристик разомкнутой системы полезно представить W(s) в виде произведения передаточных функций 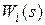 элементарных звеньев (см. подразд. 2.5), т.e.
элементарных звеньев (см. подразд. 2.5), т.e. 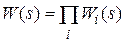 . В этом случае
. В этом случае 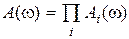 ,
, 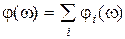 ,
, 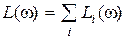 , что может существенно облегчить вычисление и построение характеристик. Если
, что может существенно облегчить вычисление и построение характеристик. Если 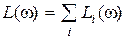 , то каждую элементарную характеристику
, то каждую элементарную характеристику 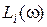 строят в виде отрезков ломаных (асимптот) и далее производят суммирование. Отметим, что первая низкочастотная асимптота определяется выражением
строят в виде отрезков ломаных (асимптот) и далее производят суммирование. Отметим, что первая низкочастотная асимптота определяется выражением 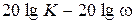 – это есть прямая с наклоном (
– это есть прямая с наклоном ( 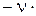 20 дБ/дек), проходящая при
20 дБ/дек), проходящая при 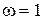 через точку с координатой
через точку с координатой 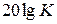 .
.
Рассмотрим теперь частотные характеристики замкнутой системы. Их можно получить по передаточным функциям замкнутой системы 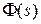 ,
, 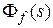 ,
, 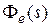 . Чаще всего рассматривают частотные характеристики на базе главной передаточной функции замкнутой системы
. Чаще всего рассматривают частотные характеристики на базе главной передаточной функции замкнутой системы 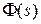 . Из них обычно используются
. Из них обычно используются 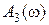 =
= 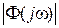 – АЧХ и
– АЧХ и 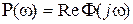 – вещественная частотная характеристика замкнутой системы.
– вещественная частотная характеристика замкнутой системы.
Остановимся на основных свойствах 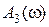 и
и 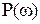 . Для физически реализуемых систем
. Для физически реализуемых систем 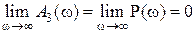 . Начальные значения этих характеристик будут
. Начальные значения этих характеристик будут
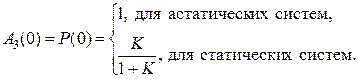
Между частотными характеристиками разомкнутой и замкнутой системы существует однозначная связь, которая следует из выражения
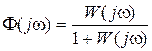 . (3.7)
. (3.7)
Представляя 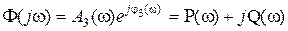 и
и 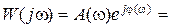
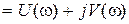 , из (3.7) можно получить следующие выражения:
, из (3.7) можно получить следующие выражения:
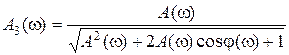 ,
, 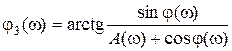 ,
,
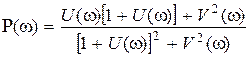 ,
, 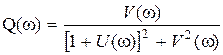 ,
,
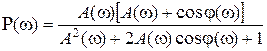 ,
, 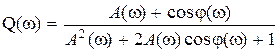 .
.
Эти выражения можно использовать для вычисления частотных характеристик замкнутой системы по частотным характеристикам разомкнутой. Существуют специальные номограммы, решающие такие задачи графически.
Дата добавления: 2015-02-07; просмотров: 1229;
