Передаточная функция и временные характеристики звеньев
Основной характеристикой звена САУ является его дифференциальное уравнение. Однако наряду с ним в теории управления нашли применение и другие характеристики. Важнейшей из них является передаточная функция, получаемая на основе применения преобразования Лапласа к исходному дифференциальному уравнению звена. Прямое и обратное преобразования Лапласа определяются следующими выражениями: 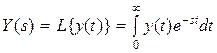 ;
; 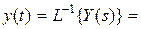
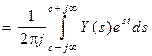 , где y(t) – оригинал; Y(s) – изображение функции y(t); s – комплексная переменная;
, где y(t) – оригинал; Y(s) – изображение функции y(t); s – комплексная переменная; 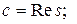
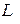 и
и 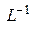 – символы прямого и обратного преобразования Лапласа.
– символы прямого и обратного преобразования Лапласа.
Наиболее важные свойства преобразования Лапласа, а также соответствие между рядом оригиналов и изображений приведены в приложении.
Если в дифференциальном уравнении звена (2.1)положить 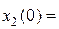
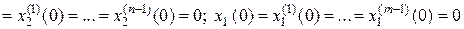 , то после применения прямого преобразования Лапласа получим алгебраическое уравнение относительно изображений:
, то после применения прямого преобразования Лапласа получим алгебраическое уравнение относительно изображений: 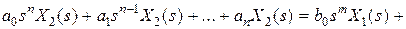
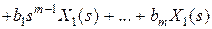 , откуда
, откуда
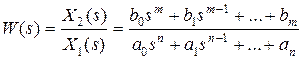 . (2.7)
. (2.7)
Пepeдаточная функция звена W(s) есть отношение изображения выходного сигнала к изображению входного сигнала при нулевых начальных
условиях.
Если взять дифференциальное уравнение звена в операторной форме (2.3), то формально W(s) получим делением оператора B(p) на оператор A(p) с заменой p на s:  .
.
Из (2.7) следует связь изображений входа и выхода через передаточную функцию:
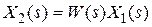 . (2.8)
. (2.8)
Звено САУ на структурных схемах изображают так, как показано на рис. 2.3.
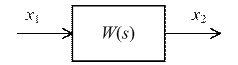 Рис. 2.3
Рис. 2.3
| При использовании уравнения (2.2)передаточную функцию звена будем записывать в виде |
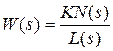 , (2.9)
, (2.9)
где N(s) и L(s) – многочлены с единичными коэффициентами в младших
членах.
Полином L(s) будем называть xapактepистичecким полиномом, а уравнение 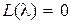 – характеристическим уравнением звена.
– характеристическим уравнением звена.
Следующий класс характеристик звена – это временные характеристики: весовая и переходная функции звена.
Если рассматривать W(s) как изображение, то приходим к понятию весовой (импульсной) функции звeнa w(t), формально определяемой как обратное преобразование Лапласа от передаточной функции
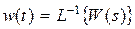 . (2.10)
. (2.10)
Вeсовая функция звена w(t) ecть реакция звена на входной сигнал в виде дельта-функции, которая определяется соотношением
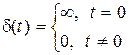 ,причем
,причем 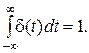
Дельта-функция обладает фильтрующим свойством: 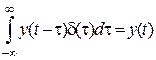 .
.
Если положить 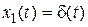 , то
, то 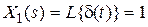 и
и 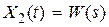 , откуда
, откуда 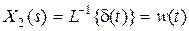 , т.е.
, т.е. 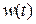 – реакция звена на входной сигнал
– реакция звена на входной сигнал 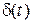 .
.
К такому же результату можно прийти следующим образом. Правой части (2.8) соответствует в области оригиналов свертка функций 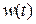 и
и 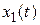 :
:
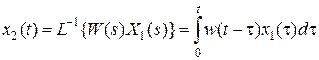 . (2.11)
. (2.11)
Если в (2.11) положить  ,то на основании фильтрующего свойства дельта-функции будем иметь
,то на основании фильтрующего свойства дельта-функции будем иметь 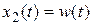 .
.
Пepexодной функциeй звена 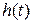 называется реакция звена на единичное ступенчатое воздействие
называется реакция звена на единичное ступенчатое воздействие 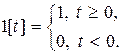
Так как 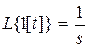 , то
, то 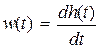 и по определению
и по определению
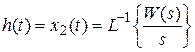 . (2.12)
. (2.12)
Так как 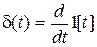 , тo
, тo 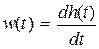 , а
, а 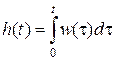 .
.
Пример 2.3. Дифференциальное уравнение двигателя постоянного тока (пример 2.1) по углу поворота в предположении, что 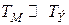 , можно записать в виде
, можно записать в виде 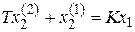 , где принято
, где принято 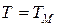 .
.
Передаточная функция и временные характеристики будут иметь вид
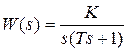 ,
, 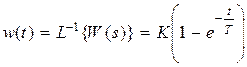 ,
,
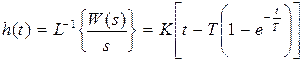 .
.
Дата добавления: 2015-02-07; просмотров: 954;
