Линеаризация уравнений динамики звеньев
Реальные устройства САУ обычно являются нелинейными. Однако при определенных условиях их можно заменить линейными моделями, что значительно упрощает исследование САУ. Операция замены нелинейных уравнений линейными носит название линеаризации. Существуют различные способы линеаризации уравнений динамики. Наиболее распространенным является способ, базирующийся на разложении нелинейных функций в ряд Тейлора.
Пусть звено CAУ описывается нелинейным дифференциальным
уравнением
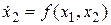 , (2.4)
, (2.4)
где 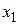 – входной, a
– входной, a 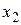 – выходной сигналы.
– выходной сигналы.
Рассмотрим установившийся режим работы звена, когда на входе действует постоянный сигнал 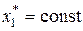 . Тогда существует постоянное значение выходного сигнала
. Тогда существует постоянное значение выходного сигнала 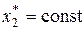 , которое можно найти из уравнения (2.4),полагая
, которое можно найти из уравнения (2.4),полагая 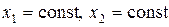 (очевидно,
(очевидно, 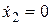 ). Связь установившихся значений сигналов х1 и х2 будет задаваться уравнением установившегося режима
). Связь установившихся значений сигналов х1 и х2 будет задаваться уравнением установившегося режима
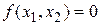 , (2.5)
, (2.5)
из которого при заданном 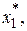 можно найти величину
можно найти величину  .
.
Введем отклонения от установившегося режима  ,
, 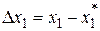 и разложим функцию f в (2.4)вряд Тейлора относительно координат
и разложим функцию f в (2.4)вряд Тейлора относительно координат 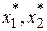 :
:
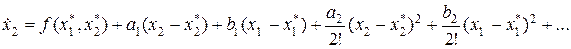 ,
,
| где | 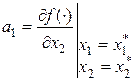 , ,
| 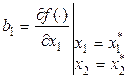
| и т.д. |
Учитывая, что 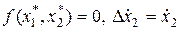 , и ограничиваясь в ряде Тейлора только линейным членом, получим
, и ограничиваясь в ряде Тейлора только линейным членом, получим
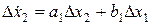 . (2.6)
. (2.6)
Уравнение (2.6) является линейным дифференциальным уравнением с постоянными коэффициентами и носит название линeаpизованного уpавнeния.
Приведенной процедуре линеаризации можно дать геометрическую интерпретацию. Уравнение установившегося режима (2.5) определяет нелинейную статическую характеристику звена (рис. 2.2).
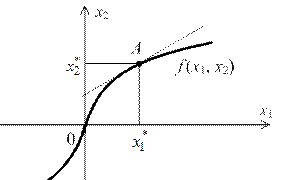 Рис. 2.2
Рис. 2.2
| Нелинейная функция 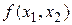 вточке разложения с координатами вточке разложения с координатами 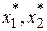 аппроксимируется линейной: касательной в точке разложения.
Отметим ряд существенных моментов в процедуре линеаризации.
1. Линеаризация допустима, если нелинейная функция аппроксимируется линейной: касательной в точке разложения.
Отметим ряд существенных моментов в процедуре линеаризации.
1. Линеаризация допустима, если нелинейная функция 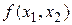 вточке разложения является аналитической (т.е. дифференцируема бесконечное число раз). Для звена, имеющего статическую вточке разложения является аналитической (т.е. дифференцируема бесконечное число раз). Для звена, имеющего статическую
|
характеристику с разрывом, линеаризация недопустима. САУ, содержащие такие звенья, должны рассматриваться как нелинейные.
2. Коэффициенты  линеаризованного уравнения (2.6) зависят от координат точки разложения
линеаризованного уравнения (2.6) зависят от координат точки разложения 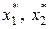 . Изменение координат дает уравнение с другими коэффициентами.
. Изменение координат дает уравнение с другими коэффициентами.
3. Линеаризованное уравнение (2.6) и исходное (2.4) будут близки между собой только в окрестности точки разложения. это соответствие будет тем лучше, чем меньше отклонения 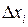 координат от установившегося режима
координат от установившегося режима
и чем ближе нелинейная функция 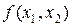 в точке разложения к своей
в точке разложения к своей
касательной. Дать определенные количественные оценки такой близости
затруднительно.
рассматриваемые далее САУ будем полагать линейными, считая, что их звенья, если это необходимо, на предварительном этапе подверглись процедуре линеаризации.
Пример 2.2. Пусть звено описывается нелинейным дифференциальным уравнением 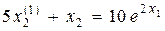 .
.
Уравнение статики имеет вид 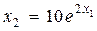 . Положим входной сигнал
. Положим входной сигнал 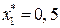 , тогда очевидно, что
, тогда очевидно, что 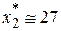 . Линеаризация исходного уравнения дает
. Линеаризация исходного уравнения дает
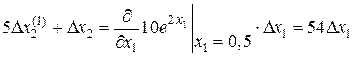 .
.
Если 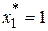 , то получим уравнение
, то получим уравнение  .
.
Таким образом, в зависимости от координат точки разложения будем иметь уравнения с различными коэффициентами.
Дата добавления: 2015-02-07; просмотров: 1168;
