Исходные данные для кинематического расчета механизма
Линейные размеры звеньев механизма:
lAB=0.117 м, , xC=0 м,
lCD=0.728 м, yC =-0.38 м,
lCS3 = 0.364 м, yE=0.71 м.
В заданном положении механизма:
угловая скорость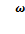 
1 = 6.44 рад/с;
угловое ускорение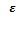 
1 = 0 рад/с2.
Угловая координата кривошипа 
1 = 150° .
Пример кинематического анализа механизма
Построение плана положений.
Планом положений механизма называется векторная диаграмма, на которой в масштабе изображены векторы звеньев механизма. При построении плана положений звенья изображаются прямыми линиями и нумеруются звенья, кинематические пары. С помощью плана положений графически решается задача о положении звеньев, определяются неизвестные линейные и угловые координаты и выясняются габариты механизма в промежуточных положениях. При выполнении расчетно-графической работы построение плана положений заменяют вычерчиванием кинематической схемы механизма в заданном положении.
Кинематической схемой механизма называется его структурная схема, выполненная в масштабе. При вычерчивании кинематической схемы используются условные обозначения звеньев и кинематических пар рекомендуемые ГОСТ 2.770-80.
Масштаб плана положений вычислим по формуле:
,
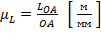где LOA- реальный размер кривошипа,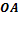 
– отрезок, отображающий кривошип на плане положений.
Кинематическая схема анализируемого механизма приведена на рис. 1.1.
Построение плана скоростей.
Планом скоростей называется векторная диаграмма скоростей механизма, построенная в масштабе относительно полюса. Полюс плана скоростей - pᵥ.
Ведущие звенья плоских механизмов свершают либо вращательное, либо поступательное движения, которые могут быть заданы или легко определяются.
Абсолютная скорость любой точки промежуточных звеньев определяется согласно теореме о скорости точки относительно полюса О:
,
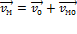где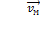 
- скорость точки М,
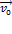– скорость полюса О,
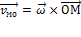– скорость вращения точки М относительно полюса.
Линейную скорость точки А звена 1 определяем по формуле вращательного движения:
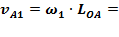8 · 0.4= 3.2 м/с.
На плане скорость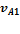 
изображается отрезком pva. Зададимся величиной этого отрезка pvа= 76 мм , и определим масштаб плана скоростей:
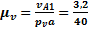= 0,08 
.
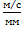Для определения скорости точки А звена 3 составим два векторных уравнения сложного движения относительно полюса А1и стойкиВ:
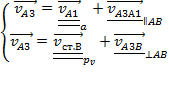
ПРИМЕЧАНИЕ: Значение символов векторных уравнений:
«_» - вектор известен по направлению,
«=» - вектор известен по модулю и направлению,
«а» - буква рядом с двойной линией подчеркивания указывает точку, из которой ведется построение следующего вектора,
«⊥AB», «ǁAB» - символы рядом с линией подчеркивания указывают линию действия вектора скорости.
Построение этой системы векторных уравнений дает графическое решение для неизвестных скоростей:
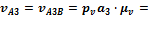36·0,08 = 2.88 м/с,
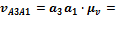13·0,08 = 1.04 м/с.
Скорость точки D и центра масс звена 3 определяем пропорциональным делением отрезков плана скоростей:
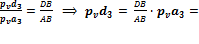54 мм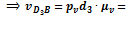 
54· 0,08 =4,32 м/с,
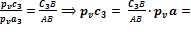22,5 мм 
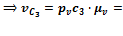22,5· 0,08 =2,16 м/с
Угловая скорость звена 3 сонаправлена вращательной скорости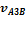 
и направлена по часовой стрелке, ее модуль находим по следующей формуле:
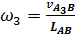= 2.88/0.9 = 3.2 рад/с,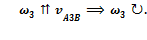 
Для определения скорости точки D звена 5 составим векторное уравнение сложного движения
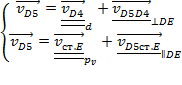
из графического решения этого уравнения находим значения скорости
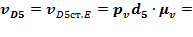51· 0,08 = 4.08 м/с,
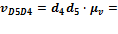16· 0,08 = 1.28 м/с.
План скоростей приведен на рис. 2.2. Векторы найденных скоростей изображены на рис. 2.3.
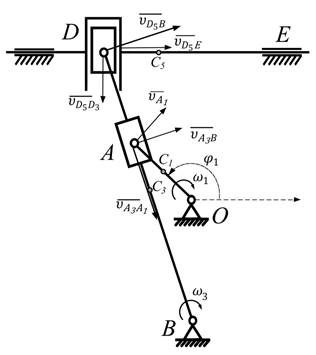
Рис. 2.2
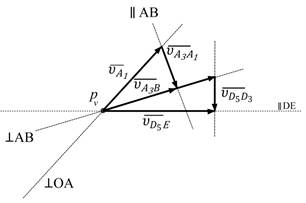
Рис. 2.3
Построение плана ускорений.
Планом ускорений называется векторная диаграмма ускорений механизма, построенная в масштабе относительно полюса. Полюс плана ускорений - pа.
Ускорения ведущих звеньев задаются или определяются исходя из того какой вид совершает первое звено.
Абсолютное ускорение любой точки промежуточных звеньев находится по теореме об ускорении точки относительно полюса:
,
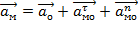где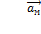 
- скорость точки М,
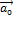– скорость полюса О,
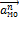– тангенциальное ускорение точки М относительно полюса О,
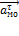– нормальное ускорение точки М относительно полюса О.
По теореме о сложении ускорений для звена, совершающего сложное движение, ускорение есть сумма переносного, относительного и ускорения Кориолиса (см. Примечания):
,
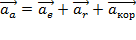здесь: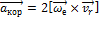 
- ускорения Кориолиса,
- угловая скорость переносного движения,
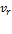– скорость относительного движения.
Ускорение точки А звена 1 определяем по формулам вращательного движения
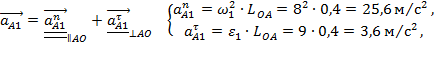
где anA1 - нормальная составляющая,
atA1 - тангенциальная составляющая ускорения.
Задаемся величиной отрезка na1 = 102,4 мм, изображающего на плане ускорений нормальную составляющую ускорение точки А, и определяем масштаб плана ускорений:
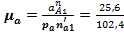= 0,25 
.
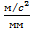Ускорение точки А звена 3 определяется совместным решением векторных уравнений сложного движения точки А3 относительно точки А1 и вращательного движения вместе со звеном 3:
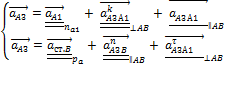
где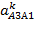 
- ускорение Кориолиса точки А3 в относительном движении относительно точки B:
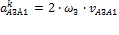= 2 · 3.2 ·1.04 = 6.656 м/с2,
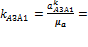6,656 ∕ 0,08 = 83,2 мм.
Полученный отрезок откладываем на перпендикуляре к АВ, построенном к точке n'a1 на плане ускорений. Направление ускорения Кориолиса находим по правилу Жуковского, которое гласит: «Проекцию вектора относительной скорости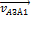 
на плоскость перпендикулярную вектору угловой переносной скорости 
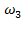поворачиваем на 90о в сторону вращения». Для плоской модели механизма всегда 
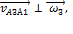взаимное расположение векторов представлено на рис.2.4.
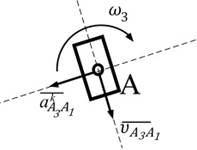
Рис. 2.4
Найдем нормальную составляющую ускорения А3 при вращательном движении вместе со звеном 3:
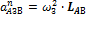= (3.2)2·0. 9 = 9.216 м/с2,
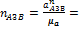9.216 ∕ 0,25 = 36.864 мм.
Полученный отрезок откладываем на параллели АВ, построенной от полюса ускорений.
Тангенциальную составляющую ускорения А3 во вращательном движении atА3В и ускорение камня вдоль кулисы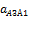 
найдем из плана ускорений:
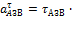
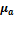= 42 
0,25 = 10,5 м/с2,
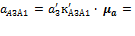57 · 0,25 = 14,25 м/с2.
По величине тангенциальной составляющей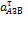 
находим угловое ускорение звена 3:
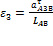= 10.5/0.9 = 12,97 рад/с2 .
Направлено угловое ускорение в ту же сторону, что и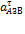 
, т.е. против часовой стрелки 
.
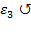Ускорение точки D и центра масс звена 3 определим методом пропорционального деления отрезков плана ускорений:
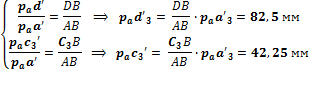
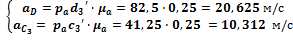
Ускорение точки D звена 5 определяется совместным решением векторных уравнений поступательного движения точки D3 относительно точки D5 и поступательного движения вместе со звеном 5:
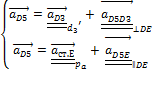
Из плана ускорений:
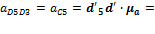72,5 ·0,25 = 18,125 м/с2 ,
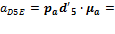41,5 · 0,25 = 10,375 м/с2 .
ПРИМЕЧАНИЕ: дополнительно находим ускорения центров тяжести каждого звена, т.к. эти значения необходимы при силовом расчете для вычисления инерционных сил.
Векторы найденных скоростей изображены на рис. 2.5. План ускорений показан на рис. 2.6.
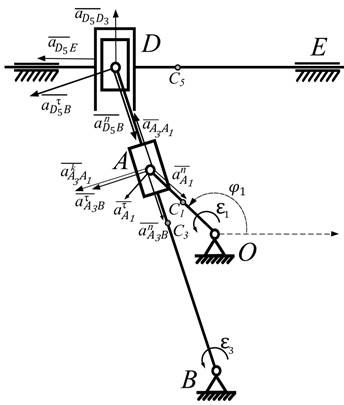
Рис. 2.5
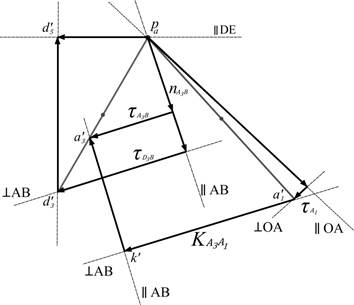
Рис. 2.6
2.2. Вопросы для самопроверки
1. Что представляют собой план положений, пан скоростей и ускорений?
2. Чем отличаются структурная и кинематическая схема механизма?
3. Как определяются абсолютная скорость и ускорение промежуточных звеньев?
4. В каком случае возникает ускорение Кориолиса? Как определить его модуль и направление?
5. Напишите векторные уравнения для любой точки промежуточного звена.
6. Зачем находят ускорения центров тяжести звеньев?
7. Как определяют угловые ускорения звеньев, в сложном и вращательном движении?
3. Динамический анализ механизма.
Динамическим анализом механизма называется силовой расчет усилий в кинематических парах без учета трения (в первом приближении) методом кинетостатики. Это необходимо для определения динамической нагрузки звеньев и кинематических пар при синтезе или анализе механизмов, т.к. на основе полученных значений рассчитывается прочность, жесткость и долговечность элементов механизма.
Статический расчет проводится при учете активных сил (внешних и сил тяжести звеньев), а кинетостатический расчет учитывает также инерционные силы и моменты. И в том и в другом случае определяются реакции в кинематических парах.
При синтезе механизма силовой расчет основывается на решении прямой (первой) задачи динамики: по заданному закону движения определить действующие силы.
При анализе механизма динамический расчет базируется на решении обратной (второй) задачи динамики: по заданным внешним силам, приложенным к звеньям механизма, определить закон движения.
При решении обеих задач используется принцип Д'Аламбера (см. Примечания), согласно которому звено механизма может рассматриваться как находящееся в равновесии, если ко всем внешним силам, действующим на него, добавить силы инерции.
В методе кинетостатики ускоренное движение звеньев учитывается, условно прикладываемыми к каждому подвижному звену механизма главного вектора инерции Фи и главного момента Мф сил инерции.
Для расчета механизм разбивается на группы Ассура и ведущее звено, расчет начинается с группы, наиболее удаленной от ведущего звена.
Для каждого звена можно записать два векторных уравнения квазиравновесия:
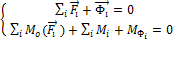(3.1)
В проекциях на оси уравнения равновесия звеньев называются уравнениями кинетостатики:
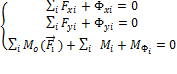(3.2)
Главный вектор Фи и главный момент Мф сил инерции звена i определяются по уравнениям:
, 
.
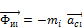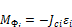Главный вектор сил инерции Фи приложен к центру масс Ci и момент инерции i-го звена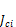 
находится относительно этой же точки.
Следует подчеркнуть, что в действительности никакой силы Фи и никакой пары сил Мф, приложенных к звену i, не существует. Главный вектор и главный момент сил инерции не имеют никакого физического содержания и в расчетных уравнениях выполняют роль чисто математических величин, посредством которых учитывается влияние ускоренного движения звеньев.
Искомые силы в кинематических парах, определяют из уравнений (3.2), в которых они содержатся в составе сумм. Поскольку значения Фи и Мф зависят от ускорений, то определяемые силы также зависят от aciи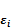 
. Следовательно, для проведения силового расчета необходимо знать закон движения механизма.
Рассмотрим действие сил в кинематических парах, считая, что влияние трения мало и им можно пренебречь.
Поступательная пара. Сила взаимодействия звеньев, образующих низшую пару, представляет собой равнодействующую элементарных сил, распределенных по поверхности соприкосновения звеньев, которая при отсутствии трения направлена по общей нормали к их поверхности.
Сила F12, приложена к звену 1 от стойки 2, направлена по нормали п—п (рис. 3.1, а). Модуль силы F12 и расстояние b неизвестны и должны быть определены в процессе силового расчета. Сила F21приложена к стойке 2 от звена 1, так как силы взаимодействия F12 и F21 по третьему закону Ньютона: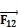 
= - 
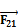
Таким образом, поступательная пара в любом случае вносит в расчетные уравнения две неизвестные величины.
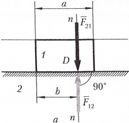
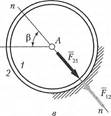
Рис. 3.1
Вращательная пара. Сила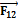 
направлена по нормали к цилиндрической поверхности соприкосновения обоих звеньев, т.е. проходит через центр шарнира А (рис. 3.1, в). Положение центра шарнира всегда известно, но модуль силы 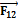и угол β неизвестны. Следовательно, вращательная пара приносит в расчет две неизвестные (они могут быть заменены двумя проекциями силы F12x и F12y).
Высшая пара. Контакт звеньев может быть либо точечным, либо линейным. При точечном контакте силовое взаимодействие звеньев выражается в виде сосредоточенной силы, при линейном — в виде распределенной нагрузкипо линии контакта. ее заменяют равнодействующей сил взаимодействия.
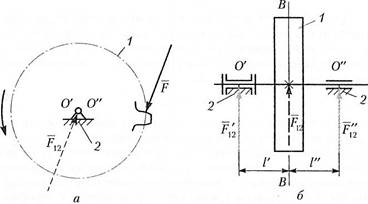
Сила F12 в высшей паре направлена по общей нормали п—п (рис. 3.2). Следовательно, для силы F12 известны точка приложения (точка контакта) и линия действия, неизвестным остается только модуль. Таким образом, в расчетных уравнениях (3.2) члены, образованные силами взаимодействия в высших парах, содержат по одному неизвестному.
|
Рис. 3.2
Дата добавления: 2015-02-05; просмотров: 1726;