Построение графиков, диаграмм.
Чаще всего применяются следующие виды графиков: график с временной шкалой, гистограммы, диаграммы.
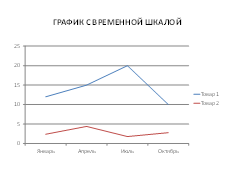
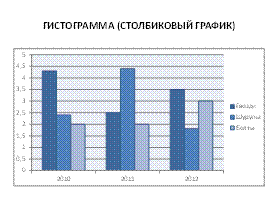
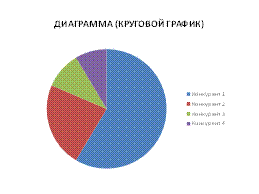
3. Вычисление статистических показателей:
3.1. Вычисление средней величины:
Средняя величина – типичный уровень явления в конкретных условиях места и времени.
- средняя арифметическая простая (используется, если данные не сгруппированы):
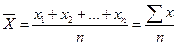 ,
,
где 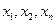 - индивидуальное значение признака,
- индивидуальное значение признака, 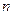 - число единиц совокупности.
- число единиц совокупности.
Пример: определить средний возраст студентов
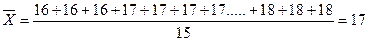 лет
лет
- средняя арифметическая взвешенная (для сгруппированных данных):
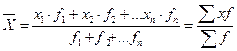 ,
,
где 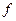 - частота повторения одинаковых значений
- частота повторения одинаковых значений
Пример:
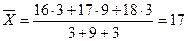 лет
лет
- Вычисление средней из интервального ряда имеет свои особенности. Сначала определяется средняя для каждого интервала по формуле средней арифметической простой как полусумма верхней и нижней границ интервала, а затем по формуле средней арифметической взвешенной рассчитывается средняя для всего ряда.
Для интервальных рядов с открытыми интервалами необходимо определить неизвестные границы: если отсутствует нижняя граница первого интервала, то его ширина принимается равной интервалу последующей группы: если отсутствует верхняя граница последнего интервала, то его ширина принимается равной интервалу предыдущей группы. Средняя для всего ряда рассчитывается по формуле:
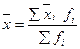
__
xi – интервальная средняя; fi –частота группы или интервала.
Пример: найти средний возраст жителя населенного пункта по следующим данным.
Распределение жителей населенного пункта по возрасту
| Возраст жителей, x | Число жителей, тыс.чел., f | __ хi |
| До 20 | 8 | 15 |
| 20-30 | 12 | 25 |
| 30-50 | 25 | 40 |
| 50-70 | 15 | 60 |
| Свыше 70 | 10 | 80 |
| Итого | 70 |
1. Находим границы открытых интервалов:
- нижняя граница первого интервала: 10,
- верхняя граница последнего интервала: 90.
2. Находим средние для каждого интервала (третий столбец).
3. Находим общую среднюю величину для всего ряда:
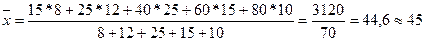
. Средняя геометрическая исчисляется извлечением корня степени n из произведений отдельных значений – вариантов признака х:
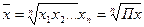
n – число вариантов, П – знак произведения.
Средняя геометрическая используется для вычисления средних из относительных величин.
3.2. Мода, 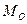 – значение, наиболее часто повторяющееся в изучаемой совокупности. Определяются по значению признака, имеющего наибольшую частоту (повторяемость).
– значение, наиболее часто повторяющееся в изучаемой совокупности. Определяются по значению признака, имеющего наибольшую частоту (повторяемость).
Пример:
16,17,17,17,17,18,17,16,17,18,16,18,17,17,17
Мода = 17 лет.
В данной группе студентов наибольшее количество студентов находятся в возрасте 17 лет.
2,4,5,5,6,6,5,6,6,7,7,8,8,9,10,11,4,3,3,4,4,5
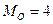 ,
, 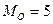 ,
, 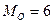 . В данной бригаде наибольшее число рабочих имеют стаж работы 4, 5 и 6 лет.
. В данной бригаде наибольшее число рабочих имеют стаж работы 4, 5 и 6 лет.
Для интервальных рядов распределения сначала определяется модальный интервал по наибольшей частоте, а внутри интервала мода рассчитывается по формуле:
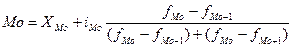
XMo – нижняя граница модального интервала,
i Mo – величина модального интервала,
fMo, fMo-1, fMo+1 – частоты в модальном, предыдущем и следующим за модальным интервалах.
3.2. Медиана, 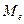 – значение, выше и ниже которого располагается по половине значений исследуемой совокупности.
– значение, выше и ниже которого располагается по половине значений исследуемой совокупности.
Для нахождения медианы все значения сначала необходимо расположить в порядке возрастания.
Для рядов, имеющих нечётное число членов, медианой является значение, находящееся в середине ряда.
16, 16, 16, 17, 17, 17, 17, 17, 17, 17, 17, 17, 18, 18, 18.
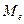
Половина студентов группы находиться в возрасте до 17 лет, другая половина более 17 лет.
Если ряд состоит из чётного числа членов, то медиана – среднее арифметическое из двух значений, расположенных в середине ряда.
Пример:
2,3,3,4,4,4,4,5,5,5,5,6,6,6,6,7,7,8,8,9,10,11
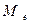
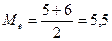
Половина рабочих бригады имеют стаж менее 5,5 лет, другая половина рабочих больше этого срока.
В интервальных рядах распределения сначала находят медианный интервал. Этот интервал характерен тем, что его кумулятивная частота (накопленная сумма частот) равна или превышает полусумму всех частот ряда. Затем внутри медианного интервала определяют медиану по следующей формуле:
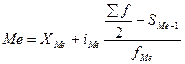
XMе – нижняя граница медианного интервала,
i Mе – величина медианного интервала,
Σf/2 – половина от общего числа наблюдений;
SMe-1 – сумма наблюдений, накопленная до начала медианного интервала;
fMе – число наблюдений в медианном интервале.
3.4. Размах вариации – разница между максимальным и минимальным значением.
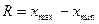
3.5. Среднее линейное отклонение представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариант от их средней арифметической:
- для несгруппированных данных:
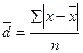
n – число членов ряда;
- для сгруппированных данных:
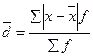
Σf – сумма частот вариационного ряда.
Разности в числителях взяты по модулю.
Среднее линейное отклонение показывает, насколько в среднем величина изучаемого признака у отдельных единиц совокупности отличается от среднего значения признака в совокупности.
3.6. Коэффициент вариаций используется для оценки однородности совокупности. Чем он больше, тем менее однородна совокупность по своему составу. Однородная - до 33 %, более 33 % - неоднородная.
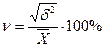
Дата добавления: 2015-02-05; просмотров: 1177;
