Анализ динамических рядов
Данные, характеризующие изменение явлений во времени, называются динамическим рядом.
Пример:
Совокупный выпуск продукции предприятием «Восток», млн.руб.
| Годы | Выпуск, млн.руб. | 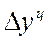
| 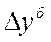
| 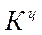
| 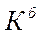
| 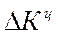
| 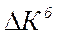
| А% |
| 2006 | 10 | - | - | - | - | - | - | - |
| 2007 | 13 | 3 | 3 | 1,3 | 1,3 | 0,3 | 0,3 | 0,1 |
| 2008 | 17 | 4 | 7 | 1,307 | 1,7 | 0,307 | 0,7 | 0,13 |
| 2009 | 22 | 5 | 12 | 1,294 | 2,2 | 0,294 | 1,2 | 0,17 |
| 2010 | 25 | 3 | 15 | 1,136 | 2,5 | 0,136 | 1,5 | 0,22 |
| 2011 | 25 | 0 | 15 | 1,0 | 2,5 | 0,0 | 1,5 | - |
| 2012 | 20 | -5 | 0,8 | 2,0 | -0,2 | 1,0 | 0,25 | |
| Σ=10 | П=1,998 |
4.1. Абсолютный прирост определяется как разность между двумя уровнями динамического ряда и показывает увеличение или уменьшение уровня ряда за определенный промежуток времени:
- абсолютный прирост цепной:
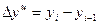
- абсолютный прирост базисный:
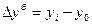
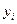 - уровень сравниваемого периода;
- уровень сравниваемого периода;
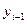 - уровень предшествующего периода;
- уровень предшествующего периода;
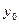 - уровень базового периода.
- уровень базового периода.
Между цепными и базисными абсолютными приростами существует следующая взаимосвязь: сумма цепных абсолютных приростов равны базисному, то есть общему приросту за весь промежуток времени:
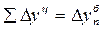
4.2. Темп роста определяется как отношение двух сравниваемых уровней и показывает, во сколько раз данный уровень превышает уровень базисного периода:
- темп роста цепной:
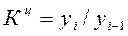
- темп роста базисный:
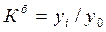
Между цепными и базисными темпами роста существует следующая взаимосвязь: произведение цепных темпов роста равны базисному за весь период:
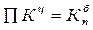
4.3. Темп прироста показывает относительное изменение величины абсолютного прироста, то есть на сколько процентов уровень данного периода больше (или меньше) уровня, принятого за базу сравнения:
- темп прироста цепной:
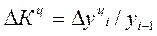
- темп прироста базисный:
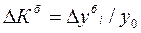
Если предварительно были рассчитаны темпы роста, то темпы прироста можно найти следующим образом:
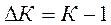
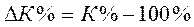
4.4. Средний абсолютный прирост может быть рассчитан двумя способами:
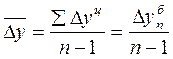
Показывает, насколько в среднем изменялся показатель за единицу времени.
4.5. Средний темп роста может быть рассчитан двумя способами:
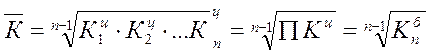
Показывает, во сколько раз в среднем изменялся показатель за единицу времени.
Пример:
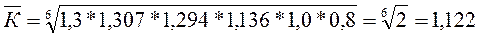
4.6. Для среднего темпа прироста сохраняет силу та же взаимосвязь, имеющая место между обычными темпами роста и прироста:
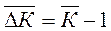
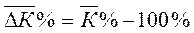
Показывает, на сколько в среднем процентов менялся показатель за единицу времени.
5. Анализ структуры
5.1. Относительная величина структурыхарактеризуют состав изучаемой совокупности и показывают, какой удельный вес или долю в общем итоге составляет каждая ее часть. Их получают путем деления значений каждой части совокупности на их общий итог, принятый за базу сравнения (например, удельный вес городского населения в общей численности населения РФ).
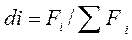
Fi - показатель, характеризующий часть совокупности, ∑Fi - показатель, характеризующий всю совокупность в целом.
5.2. Относительная величина координации характеризуют отношение отдельных частей целого, одна из которых принимается за базу сравнения (отношение мужской части населения к женской).
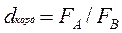
Fa - показатель, характеризующий часть совокупности, Fb - показатель, характеризующий часть совокупности, принятую в качестве базиса.
Способы анализа качественных данных:
Дата добавления: 2015-02-05; просмотров: 1182;
