Модуль 2. Молекулярная физика и термодинамика. Электромагнетизм
Лекция 8 Молекулярная физика
План
1. Средняя кинетическая энергия молекул идеального газа. Газовые законы, уравнение состояния идеального газа.
2. Распределение Максвелла. Скорости теплового движения частиц. Распределение Больцмана для частиц во внешнем потенциальном поле. Число степеней свободы.
Тезисы
1. Молекулярная физика и термодинамика — разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в телах атомов и молекул. Для исследования этих процессов применяют два качественно различных и взаимно дополняющих друг друга метода: статистический (молекулярно-кинетический) и термодинамический. Первый лежит в основе молекулярной физики, второй — термодинамики. Молекулярная физика — раздел физики, изучающий строение и свойства вещества исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном хаотическом движении.
Молярная масса (масса 1 моль вещества) 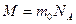 Молярный объем
Молярный объем 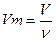 Количество вещества
Количество вещества 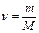 Концентрация (количество молекул в 1м3)
Концентрация (количество молекул в 1м3) 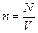 ,
, 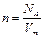
Постоянная Авогадро: nа = 6 • 1023 моль-1 (число молекул в 1 моле вещества)
Молярная газовая постоянная (универсальная): R = p0V0/T0 = 8,31 Дж / (моль•К)
Постоянная Больцмана (универсальная): k = R / NА = 1,38 • 10-23 Дж / К
Число Лошмидта: NL = p0 / (kT0) = 2,68 • 1025 м-3 (число молекул, содержащихся в 1 м3 газа при н.у.)
Законы, описывающие поведение идеальных газов (газовые законы)
1. Закон Бойля — Мариотта: для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная: pV = const при Т = const, m = const
2. Закон Гей-Люссака для изобарного процесса: объем данной массы газа при постоянном давлении изменяется линейно с температурой: V=V0 ( 1+a t ) при p = const, m = const или V1 / V2 = T1 / T2 при p = const, m = const, где V0 – объем при 00С, 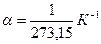
3. Закон Гей-Люссака для изохорного процесса: давление данной массы газа при постоянном объеме изменяется линейно с температурой: p = p0 ( 1+a t ) при V = const, m = const или р1 / р2 = T 1/ T2 при V = const, m = const , где p0 – объем при 00С, 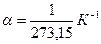
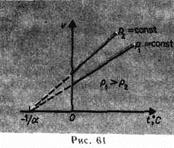
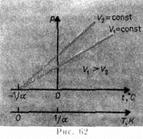
4. Закон Авогадро: моли любых газов при одинаковых температуре и давлении занимают одинаковые объемы. При нормальных условиях (сокращенно: при н.у.) (р0 = 105 Па, T0 = 273 K) этот объем равен 22,41 • 10-3 м3/моль.
5. Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов: p = p1 + p2 + ... + pn , где p1,p2, ..., pn — парциальные давления — давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
Уравнение Клапейрона (уравнение состояния идеального газа) 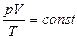 Уравнение Клапейрона-Менделеева
Уравнение Клапейрона-Менделеева 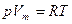 или
или 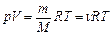 или
или 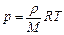 или
или 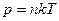
Основное уравнение кинетической теории газов
Кинетическая теория газов основана на следующих общих положениях классической статистической физики: в системе выполняются законы сохранения импульса, момента импульса, энергии, электрического заряда; предполагается возможность отличать друг от друга тождественные частицы; все физические процессы в системе протекают в пространстве и времени непрерывно; каждая частица системы может иметь произвольные значения координат и компонент скорости независимо от того, каковы значения этих характеристик у других.
Основное уравнение кинетической теории газов 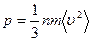 Средняя кинетическая энергия поступательного движения одной молекулы
Средняя кинетическая энергия поступательного движения одной молекулы 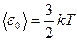 Число степеней свободы молекулы – это число независимых переменных, полностью определяющих положение системы в пространстве. Обозначение: I . Для одноатомного газа (гелий, водород): i = 3, двухатомного (кислород, азот): i = 5, многоатомного (углекислый газ, атмосферный воздух): i = 6. На каждую степень свободы молекулы приходится одинаковая энергия
Число степеней свободы молекулы – это число независимых переменных, полностью определяющих положение системы в пространстве. Обозначение: I . Для одноатомного газа (гелий, водород): i = 3, двухатомного (кислород, азот): i = 5, многоатомного (углекислый газ, атмосферный воздух): i = 6. На каждую степень свободы молекулы приходится одинаковая энергия 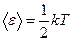
Закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT / 2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень «обладает» вдвое большей энергией потому, что на нее приходится не только кинетическая энергия (как в случае поступательного и вращательного движений), но и потенциальная, причем средние значения кинетической и потенциальной энергий одинаковы. Таким образом, средняя энергия молекулы 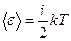 , где i — сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы: i = iпост + iвращ + 2 iколеб
, где i — сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы: i = iпост + iвращ + 2 iколеб
Внутренняя энергия идеального газа 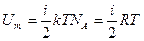 или
или 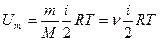
Теплоемкость 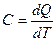 Удельная теплоемкость
Удельная теплоемкость 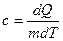 Молярная теплоемкость
Молярная теплоемкость 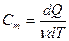 Связь между удельной и молярной теплоемкостями
Связь между удельной и молярной теплоемкостями 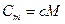
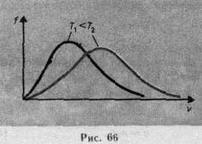
2. Законы поведения огромного числа молекул, являясь статистическими закономерностями, изучаются с помощью статистического метода. Этот метод основан на том, что свойства макроскопической системы в конечном счете определяются свойствами частиц системы, особенностями их движения и усредненными значениями динамических характеристик этих частиц (скорости, энергии и т.д.). Например, температура тела определяется скоростью беспорядочного движения его молекул, но так как в любой момент времени разные молекулы имеют различные скорости, то она может быть выражена только через среднее значение скорости движения молекул.
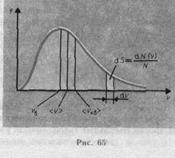
Закон Максвелла о распределении молекул идеального газа по скоростям (распределение Максвелла) 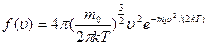 Скорости, характеризующие состояние газа
Скорости, характеризующие состояние газа
1. Наиболее вероятная скорость 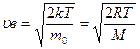 2. Средняя скорость молекулы
2. Средняя скорость молекулы 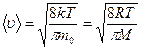 3. Средняя квадратичная скорость молекул
3. Средняя квадратичная скорость молекул 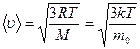
Функция распределения молекул по энергиям теплового движения 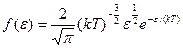 Барометрическая формула
Барометрическая формула 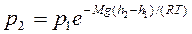 или
или 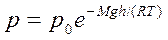 Распределение Больцмана
Распределение Больцмана 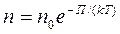 во внешнем потенциальном поле: при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.
во внешнем потенциальном поле: при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.
Дата добавления: 2015-01-29; просмотров: 1637;
