Признаки мультиколлинеарности.
1.В модели с двумя переменными одним из признаков мультиколлинеарности является близкое к единице значение коэффициента парной корреляции. Если значение хотя бы одного из коэффициентов парной корреляции больше, чем 0,8, то мультиколлинеарность представляет собой серьезную проблему.
Однако в модели с числом независимых переменных больше двух, парный коэффициент корреляции может принимать небольшое значение даже в случае наличия мультиколлинеарности. В этом случае лучше рассматривать частные коэффициенты корреляции.
2. Для проверки мультиколлинеарности можно рассмотреть детерминант матрицы коэффициентов парной корреляции |r|. Этот детерминант называется детерминантом корреляции |r| ∈(0; 1). Если |r| = 0, то существует полная мультиколлинеарность. Если |r|=1, то мультиколлинеарность отсутствует. Чем ближе |r| к нулю, тем более вероятно наличие мультиколлинеарности.
3. Если оценки имеют большие стандартные ошибки, невысокую значимость, но модель в целом значима (имеет высокий коэффициент детерминации), то это свидетельствует о наличие мультиколлинеарности.
4. Если введение в модель новой независимой переменной приводит к существенному изменению оценок параметров и небольшому изменению коэффициента детерминации, то новая переменная находится в линейной зависимости от остальных переменных
65. Фиктивные переменные: определение, назначение, типы, смысл названий.
Фиктивные переменные – это переменные с дискретным множеством значений, которые количественным образом описывают качественные признаки. В эконометрических моделях обычно используются фиктивные переменные бинарного типа “0-1”.

Фиктивные переменные необходимы для оценки качественных признаков на эндогенную переменную. Например, при оценке спроса на некоторый товар мы построили регрессионную модель, регрессорами в которой в которой были количественные переменные – цены и дохода потребителя. Одним из способов уточнения данной модели может послужить включение таких качественных признаков, как вкус потребителя, возраст, национальные особенности, сезонность и т.д. Эти показатели нельзя представить в численном виде. Поэтому возникает задача отражения их влияния на значения эндогенной переменной, которая решается как раз при помощи введения фиктивных переменных.
В общем случае, когда качественный признак имеет более двух значений, вводится несколько бинарных переменных. При использовании нескольких бинарных переменных необходимо исключить линейную зависимость между переменными, так как в противном случае, при оценке параметров, это приведет к совершенной мультиколлинеарности. Поэтому применяется следующее правило: если качественная переменная имеет k альтернативных значений, то при моделировании используются только (k-1) фиктивная переменная.
В регрессионных моделях применяются фиктивные переменные двух типов:
1. Фиктивные переменные сдвига – эти переменные применяются в динамических моделях, когда с определенного момента времени начинает действовать какой-либо качественный фактор (например, при рассмотрении производительности завода до забастовки рабочих и во время нее). Эти переменные применяются, когда изменение качественного признака приводит к параллельному сдвигу графика регрессионной модели, поэтому они и называются переменными сдвига.
2. Фиктивные переменные наклона – это переменная, которая изменяет наклон линии регрессии. При помощи таких фиктивных переменных можно построить кусочно-линейные модели, которые позволяют учесть структурные изменения в экономических процессах (например, введение новых правовых или налоговых ограничений, изменение политической ситуации и т.д.) Такие переменные применяются, когда изменение качественного признака приводит не к параллельному сдвигу графика регрессии, а к изменению его наклона. Собственно поэтому такие фиктивные переменные и называются переменными наклона.
66. Фиктивная переменная сдвига: спецификация регрессионной модели с фиктивной переменной сдвига.
Фиктивные переменные сдвига – эти переменные применяются в динамических моделях, когда с определенного момента времени начинает действовать какой-либо качественный фактор (например, при рассмотрении производительности завода до забастовки рабочих и во время нее). Эти переменные применяются, когда изменение качественного признака приводит к параллельному сдвигу графика регрессионной модели, поэтому они и называются переменными сдвига.
Спецификация парной регрессионной модели с фиктивной переменной сдвига имеет вид:
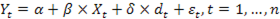
Где α, β, δ – параметры модели;  – значение регрессора в наблюдении t;
– значение регрессора в наблюдении t;
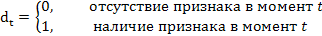
- фиктивная переменная;
δ – параметр при фиктивной переменной.
Значение фиктивной переменной dt=0 называется базовым (сравнительным). Базовое значение может либо определяться целями исследования, либо выбираться произвольно. Если заменить базовое значение переменной, то суть модели не изменится, изменится знак параметра δ на противоположный.
Рассмотрим парную регрессионную модель с фиктивной переменной сдвига на примере.
Пусть на продажи мороженого влияет наличие рекламы на фургоне у продавца. При помощи уравнения с фиктивными переменными можно, использую одно уравнение регрессии, получить результат как для продавцов с рекламой, так и для продавцов без рекламы.
Пусть первоначальная модель описывается спецификацией:

Где n – количество продавцов мороженого,  – количество продаж для t-го продавца,
– количество продаж для t-го продавца,  – значение количественного регрессора для t-го продавца
– значение количественного регрессора для t-го продавца
Введем фиктивную переменную сдвига

Спецификация примет вид:

Величина δ интерпретируется как среднее изменение продаж при переходе из группы (без рекламы) в группу (с рекламой).
Для оценки параметров модели в Excel, значения переменных будут оформлены в таком виде:
| t | Yt | Xt | dt |
| Y1 | X1 | ||
| Y2 | X2 | ||
| Y3 | X3 | ||
| … | … | … | … |
| n | Yn | Xn |
Результат оценивания

Позволяет проверить предположение о несуществующем различии в продажах между категориями 

То нулевая гипотеза не отвергается, и наличие рекламы у продавца не оказывает существенного влияния на продажи мороженого.
Дата добавления: 2015-01-10; просмотров: 3881;
