Области распространения и затухания

Дисперсионные соотношения для одноатомной одномерной цепочки известны. Частоты возможных собственных (незатухающих) мод определяются формулой

,

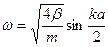
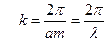где волновой вектор k задан в зоне Бриллюэна.

Для цепочки конечных размеров обычно используют циклические граничные условия Борна-Кармана, устанавливающие идентичность атома n и n+N:

U_n=A exp[i(w×t+nak)]=Aexp[i(w×t+(n+N)ak)] = U_n+N

exp[iNka]=1; Nka=2pp; p=0,1,2...N–1;

–p/a < k=p2p/Na < +p/a ; –N/2 < p < +N/2.

Таким образом, в кристалле, имеющим N элементарных ячеек, может существовать лишь N различных собственных частот (фононов). Вид дисперсионных зависимостей как функции от волновых векторов показан на рис. 4.

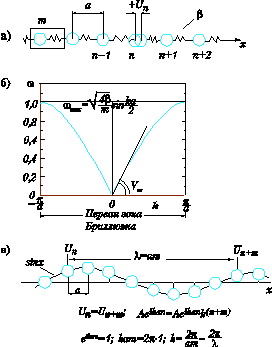
Рис. 4. Моноатомная цепочка: а) цепочка частиц массой m с периодом решетки a; б) дисперсионная зависимость w(k) для линейной моноатомной цепочки. Тангенс угла наклона дисперсионной зависимости равен скорости звука в цепочке. в) физический смысл волнового вектора k. Если найти ближайший к атому n атом n+m, имеющий то же смещение, что и атом n, т.е. потребовать выполнения U_n=U_n+m, то ясен физический смысл волнового вектора k: эта величина по модулю равна 2p¤λ, где λ=am – длина волны возбуждения.

Так как дисперсионная зависимость w(k) периодична по k с периодом 2p/a, область изменения волнового вектора k также периодична и выбирается симметричной от –p/a до +p/a, чтобы учесть волны, бегущие в противоположных направлениях. Эта область носит название первой зоны Бриллюэна. Таким образом, максимальная частота собственных колебаний системы не можен превышать w_max=(4β/m)^1/2. Волны с частотами w>w_max будут распространяться через цепочку с затуханием, поскольку при этом условии из дисперсионного соотношения следует, что sin(ka/2)>1, т.е. волновой вектор k представляет собой комплексную величину k+ia :

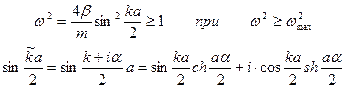
Мнимая часть этого выражения равна нулю, т.к. частота действительна. Следовательно, cos(ka/2)=0 и k=p/a, т.е. соседние частицы при таком движении колеблются в противофазе, а само движение имеет вид затухающей с коэффициентом a волны (рис. 5):

.

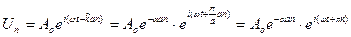Для малых волновых векторов k»0 (l®¥) движение частиц происходит в фазе с частотами, пропорциональными величине k (ka<<1). При увеличении волнового вектора до значения p/a, соответствующего границе зоны Бриллюэна, частота принимает значение w_max=(4β/m)^1/2, а на более высоких частотах волновой вектор становится комплексным k=p/a+ia, причем действительная его часть равна p/a.На графике дисперсионной зависимости (рис. 7) комплексное значение волнового вектора удобно откладывать по оси k за значением p/a, соответствующем границе зоны Бриллюэна, подчеркивая этим, что действительная его часть равна p/a.

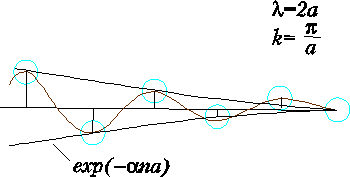
Рис. 5. Колебания моноатомной цепочки с частотами выше максимальной. Вид движений при вынужденных колебаниях цепочки с частотами w²>>w²_max=4b/m, [ w=4b/m^.sin(ka/2)].Если частота внешнего воздействия w²>>w²_max=4b/m, это означает, что волновой вектор k является комплексным числом k=k+ic, так что sin(ka/2)=sin[(k+ic)a/2]=sin(ka/2)×ch(ca/2)+i×cos(ka/2)×sh(ca/2); поскольку sin(ka/2) определяет физическую частоту w=4b/m^.sin(ka/2), и должен быть действительным числом, мнимая часть этого выражения равна нулю, что может иметь место только когда значение ka/2=p/2. Таким образом, соседние частицы колеблются в противофазе. Поэтому смещение частиц в цепочке должно иметь вид: u_n=A×exp[i(w×t+an/pa)]×exp(–can). Это показано на рисунке.

В бесконечной одномерой цепочке, элементарная ячейка которой содержит 2 частицы (см. рис. 6), существуют две ветви – акустическая и оптическая. Трехмерным аналогом такой модели могут быть кристаллы NaCl, KBr и др. Постоянная решетки a=a'/2, a' – расстояние между соседними атомами, массы частиц – m₁>m₂, упругие силовые постоянные – b₁=b₂=b. Обычно используют четную нумерацию для частиц массы m₁ и нечетную – для частиц массы m₂. Соответствующие смещения U_2n и U_2n+1. Система дифференциальных уравнений, описывающая движение частиц, имеет бесконечное число пар уравнений, имеющих для легкой и тяжелой частицы следующий вид:

.

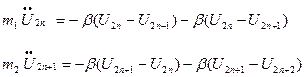Решение этой системы ищут в виде, удовлетворяющем теореме Блоха, т.е. в виде периодической функции, определенной в элементарной ячейке, домноженной на фазовый множитель expi(k,r_n):

,

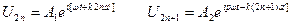где A₁ и A₂ – амплитуды смещений частиц массы m₁ и m₂, w – частота колебаний, а k – волновой вектор возбуждения.

Подстановка этих решений в бесконечную систему дифференциальных уравнений приводит eё к однородной системе из двух алгебраических уравнений относительно неизвестных амплитуд колебаний А₁ и А₂. Известно, чтобы система имела нетривиальное (ненулевое) решение, необходимо, чтобы ее детерминант равнялся нулю.

A₁(m₁w²–2b)+A₂2bcoska'=0

A₁2bcoska'+A₂(m2w²–2b)=0.

Это дает связь между частотой возбуждения w и волновым вектором k, которая, как известно, носит название дисперсионного соотношения:

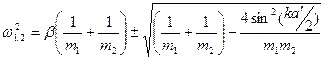(1)

Дисперсионное соотношение можно записать и так ( ибо 1-2sin²ka'=coska):

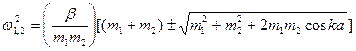. (2)

Здесь волновой вектор k принимает ряд значений в соответствии в граничными условиями задачи. Дисперсионное условие имеет два корня w₁, w₂, так что каждому значению волнового вектора k соответствует две волны. Таким образом, дисперсионная кривая имеет две ветви – акустическую (знак –) и оптическую (знак +).

Легко получить значения частот при k=0 и на границе зоны Бриллюэна (k=p/a). Для акустических колебаний это область от w_a^min=0 до w_а^max=(2b/m₁)^1/2, а для оптических это область от w_o^min=(2b/m₂)^1/2до значения w_o^max=(2b(1/m₁+1/m₂))^1/2. Если ограничиться взаимодействием лишь ближайших соседей, то ветви внутри зоны гладки. Обе ветви идут не пересекая друг друга и имеет место область запрещенных частот от значения (2b/m₁)^1/2 до (2b/m₂)^1/2.

Известно, что частоты акустической и оптической ветви вблизи границы зоны Бриллюэна меняются по параболическому закону, а групповая скорость волны на границе зоны Бриллюэна равна нулю, т.е. это стоячая волна.

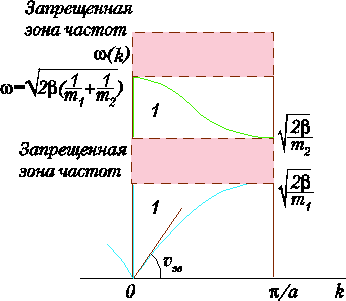
Рис. 6. Дисперсионная зависимость w(k) для двухатомной линейной цепочки. 1 – дисперсивная область, т.е. зона собственных колебательных состояний); 2 – реактивная область – красная, т.е. запрещенная зона частот.

В области запрещенных частот, т.е. в области от значения (2b/m₁)^1/2 до (2b/m₂)^1/2 и выше самой высокой частоты, равной w_o^max=(2b(1/m₁+1/m₂))^1/2, распространение механических волн будет происходить с затуханием, так как волновой вектор колебаний будет комплексным. Действительно, дисперсионное уравнение (1) можно переписать как функцию от частоты:

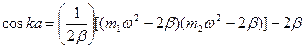(3)

Решение этого уравнения дает как действительные, так и комплексные значения волнового вектора k для любых частот. Легко проверить, что в области запрещенных частот между акустической и оптической ветвью действительная часть волнового вектора равна, как и в одноатомной цепочке, p/a, так что соседние атомы колеблются в противофазе. В области запрещенных частот выше самой высокой частоты соседние атомы колеблются в фазе, т.е. действительное часть волнового вектора равна нулю. Поэтому на графике эту часть дисперсионной зависимости рисуют слева от нуля, подчеркивая тем самым, что в этом случае имеется только мнимая часто волнового вектора. Подобный график для цепочки с массами m₁=2 и m₂=5 и силовых констант b=35000 построен на рис. 7.

Используя дисперсионное соотношение, можно построить зависимости w(k) для одномерной модели кристалла CdSe, приведенную на рис. 7. Из рисунка видно, что в нанокристалле могут существовать собственные колебания не с любыми частотами, а только с теми, которые попадают в разрешённую область либо акустических движений, либо оптических колебаний.

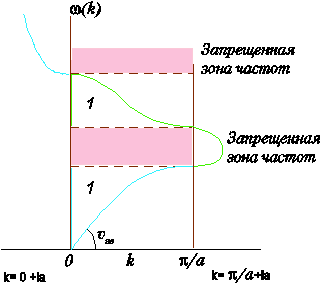
Рис. 7.Дисперсионныезависимости для одномерной модели кристалла. Рисунок содержит 3 области волновых векторов, в которых построены дисперсионные зависимости частот колебаний механической волны. Область k с действительными значениями волнового вектора k представляет собой область собственных колебаний одномерной цепочки. Смещения здесь равны: U_n= Ae^ikan Область справа представляет собой область затухающих волн с комплексным волновым вектором k =π/a+ia/a. Смещения здесь равны: U_n= Ae^iπn e^–an . В области слева от нуля существуют только затухающие колебания с чисто мнимым значением волнового вектора k = ia. Мнимая часть волнового вектора показывает, насколько быстро происходит затухание колебаний в запрещённых областях частот. Для этой модели колебания, попадающие в частотную область между акустической и оптической ветвями, затухают с волновым вектором k =π/a+i(π/2)/a, что на расстоянии 2a соответствует затуханию в e раз.

Данные колебания соответствуют фононным ветвям из области рисунка с действительными значениями волнового вектора k. Колебания из запрещённых зон (зона частот между акустической и оптической ветвью и область частот выше наибольшей собственной частоты) затухают в кристалле. Волновой вектор таких фононов имеет отличную от нуля мнимую часть. Значение мнимой части волнового вектора характеризует затухание таких колебаний. В областях 1 и 3 построены зависимости частот вынужденных колебаний кристалла от мнимых частей волновых векторов. Такие движения соответствуют затухающим колебаниям. Например, амплитуда колебания с частотой 280 cm^–1 для данной модели кристалла CdS уменьшается в e раз на расстоянии в 1 элементарную ячейку.