Сложенные (folding modes) акустические моды

Ясно, что оптические ветви механических колебаний кристалла весьма похожи на электронные зоны. Энергия, например, изменяется квадратично с волновым вектором k около критических точек, включая и точку Г (т.е. центр зоны Бриллюэна) и границу зоны Бриллюэна. Акустические ветви, однако, имеют другой вид: в любом материале частоты механических колебаний стремятся к нулю при k=0. Последнее является результатом того, что акустический фонон с k = 0 (т.е. бесконечной длиной волны) соответствует однородной трансляции кристалла. При такой трансляции не возникает возвращающей силы, поскольку расстояния между атомами не изменяются. Другая особенность, характерная для акустических фононов, заключается в том, что их дисперсия вблизи Г линейна (а не квадратична) по k, причем тангенс угла наклона дисперсионной кривой равен скорости звука в кристалле.

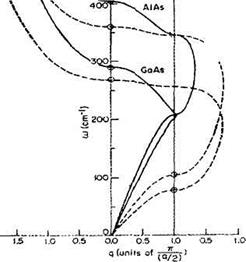
Рис. 9.Дисперсионные кривые для распространения механических волн в кристаллах GaAs и AlAs, которые являются наиболее типичными предста­вителями таких структур полупроводников A₃B₅ . Рисунок содержит 3 области волновых векторов, для которых построены зависимости частот колебаний механической волны. Область с действительными значениями волнового вектора q представляет собой область собственных колебаний одномерной цепочки. Смещения здесь равны: U_n= Ae^iqan Область справа от первой представляет собой область затухающих волн с комплексным волновым вектором q=π/a+ia/a. Смещения здесь равны: U_n= Ae^iπn e^–an. В области левее от действительных волновых векторов существуют только затухающие колебания с чисто мнимым значением волнового вектора q= ia. Мнимая часть волнового вектора показывает, насколько быстро происходит затухание колебаний в запрещённых областях частот. Для этих кристаллов области акустических колебаний перекрываются,в то время как частотные области оптических колебаний не перекрываются. Таким образом оптические колебания каждого из кристаллов в гетероструктуре (сверхрешетке) не будут распространяться в другом кристаллическом слое.

Особенности распространения акустических и оптических колебаний легко понять из рис. 9. Акустические колебания двух кристаллов всегда имеют общий спектральный интервал частот от нуля до дебаевской частоты (ω_D=v_звукаπ/a). Поэтому акустические волны будут распространяться как в одном, так и в другом материале со скоростями, соответствующими скоростям в конкретном кристаллическом слое. При этом при распространении определенной частоты длина волны в каждом материале будет своя, поскольку λ=v_звука/ω.

Подобные особенности дисперсии акустических фононов обычно препятствуютих квантованию. В обоих материалах в диапазоне частот от нуля до максимальной частоты того материала, который является более мягким в смысле упругости механические волны будут распространяться без затухания. Отметим, что в системе GaAs/AlAs (см. рис. 9) максимальные акустические частоты обоих компонент почти одинаковы, поэтому едва ли существует диапазон частот, в котором распространяющиеся акустические моды существовали бы только в одном из двух материалов. В пределах применимости теории упругости акустические фононы в сверхрешетках соответствуют упругим волнам, распространяющимся с дисперсией ω= v_звука k, где v_звука – средняя скорость звука для двух сред. Если k направлен вдоль оси роста сверхрешетки, состоящей из повторяющихся слоев среды А с толщиной d_A и среды В с толщиной d_B (период d = d_A + d_B), легко найти эту среднюю скорость. Время распространения вдоль z на расстояние периода d равно t = d_A/v_A + d_B/v_B, где v_A – скорость звука в среде A, а v_B – скорость звука в среде B. Поэтому средняя скорость звука равна:

v_звука=d/t=d(d_A/v_A+ d_B/v_B). (5)

В отличие от акустических волн оптические моды (рис. 9) образуют узкие зоны разрешенных частот с центром около 280 см^–1 в GaAs и 380 см^–1 в AlAs. В области некоторых частот, соответствующих оптическим модам в GaAs, распространяющиеся моды в AlAs отсутствуют. Вследствие этого должны возникать эффекты квантования, аналогичные эффектам квантования электронов. Однако, в отличие от случая электронов, на рис. 9 имеются моды, распространяющиеся в одном из двух материалов, но не распространяющиеся в другом: существуют GaAs-подобные моды, для которых слои AlAs ведут себя как барьеры, и AlAs-подобные моды, для которых подобно барьерам ведут себя слои GaAs. Такие квантованные оптические моды широко изучались в последние годы. На рис. 10 приведены дисперсионные кривые для кристаллов GaAs и AlAs для различных направлений распространения фононов в кристалле. Рассматривая рисунок, легко установить в каких направлениях могут распространяться фононы при напосредственном контакте этах двух кристаллов.

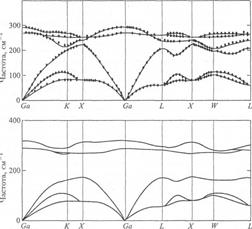
Рис. 10. Дисперсионные кривые (сплошные линии) для объемных GaAs (сверху) и AlAs (снизу). Наблюдается сильное перекрытие частот их акустических мод, в отличие от оптических мод, для которых перекрытие отсутствует. Ромбики соответствуют эксперимен­тальным данным для GaAs

Для того, чтобы проиллюстрировать эффекты распространения механических волн гетероструктуре в наиболее простом случае, рассмотрим сверхрешетку с периодом, состоящим из из двух слоев элемента А с атомной массой m_A и двух слоев элемента В с массой m_B (например, Si и Ge). Элементарная ячейка такой периодической структуры показана на рис. 11. Мы будем рассматривать только моды, распространяющиеся вдоль оси роста, и предположим, что возвращающие силы существуют лишь между соседними плоскостями с одной и той же силовой постоянной β например, между плоскостями Ge-Ge, Ge-Si и Si-Si).

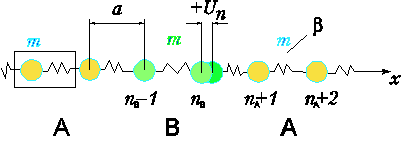
Рис. 11. Одномерная сверхрешетка, составленная из двух слоев атомов элемента A и двух слоев элемента B.

Уравнения движения для фононов с волновым вектором k, распространяющихся вдоль оси сверхрешетки, тогда имеют вид

–m_Aω²w = β[(x–w) + (uе^–idk –w)],

–m_Bω²x= β[(y – x) + (w– x)], (6)

–m_Bω²y= β[(u –y) + (x– y)],

–m_Aω²u= β[(ve^idk –u) + (y– u)].

Для того, чтобы эта система однородных линейных уравнений (относительно смеще­ний w, х, у, u пар атомов в слое с массами m_A и m_B) имела ненулевые решения, ее определитель должен быть равен нулю. Последнее приводит к секулярному уравнению четвертой степени относительно ω² для произвольного k. Его можно разбить на два квадратных уравнения, которые нетрудно решить алгебраически для центра зоны Бриллюэна (ЗБ) с k = 0 и на границе так называемой зоны Бриллюэна с k = π/d. Поскольку период сверхрешетки равен d= d₁+ d₂, зона Бриллюэна уменьшается по сравнению с зоной для объемного кристалла и носит название мини-ЗБ. Четыре разрешенных частоты при k = 0 включают ω² = 0 (акустические моды сверхрешетки) и еще три частоты:

ω² = β(1/m_A+1/m_B) (7)

ω² = β/2m_Am_B [3(m_A+m_{B)± √}9(m_A– m_B)+ 4m_Am_B] . (8)

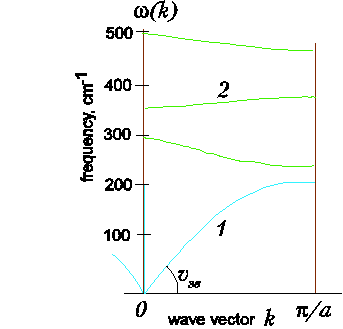
Рис. 12. Расчетные дисперсионные кривые для сверхрешетки A₂B₂ (например, Si₂Ge₂), показанной на рис.11. 1 – акустическая ветвь, определяемая средней скоростью звука в сверхрешетке, 2 – три оптические ветви.

Проще всего всего найти два раздельных квадратных уравнения для собственных значений, учитывая, что смещения фононов (собственные векторы) могут быть или нечетными, или четными относительно центра суперячейки на рис. 11. Поскольку нечетные и четные собственные векторы не смешиваются, можно разделить четыре уравнения на два не связанных набора уравнений, которые сводятся к уравнениям частот для нечетного соб­ственного вектора (плюс ω² = 0) и ко второму уравнению — для четного. Если использовать реальные соотношения между массами Ge и Si, те. предположить m_B = 2,6 m_A, что соответствует сверхрешетке Ge₂Si₂, и использовать одну из фононных частот при k = 0 объемного кристалла Ge_, равную β/m_A = (520 см^–1)² , можно найти все возможные частоты для такой сверхрешетки: ω= 348 см^–1, ω= 516 см^–1 и ω= 266 см^–1. Наиболее высокочастотная мода очень близка к моде объемного Si (520 см^–1) при k = 0, в то время как две более низкочастотные мо­ды близки к моде объемного Ge (300 см^–1). Дисперсионные кривые, полученные для рассматриваемой сверхрешетки, построены на рис. 12 для произвольного k в пер­вой зоне Бриллюэна (ЗБ) сверхрешетки (мини-ЗБ). Отметим, что вектор k на краю этой ЗБ равен половине значения, соответствующего точке X в Si (2π/d, где d = a₀). Поэтому у дисперсионных кривых, приведенных на рис. 12, число ветвей вдвое больше, чем у Si (см. рис. 10) или Ge. Чтобы отметить данный факт, говорят, что происходит сложение дисперсионных кривых (или ЗБ). Для случая m_A = m_B вместо рис. 12 мы бы получили дисперсионные кривые Г-X для объемных про­дольных фононов, сложенные посередине линии, делящей пополам отрезок оси вдоль направления Г-X. В сверхрешетках с m_A≠m_B появляются расщепления сложенных зон при k, равном 0 и n/d. Эти расщепления подобны расщеплениям, появляющимся в зонах свободных электронов вследствие периодического потенциала: модуляция массы вдоль оси роста является эквивалентом периодического потенциала.

Из приведенного выше рассмотрения следует, что две самые низкие ветви на рис. 12 можно описать как дисперсионные кривые сложенных LA фононов (folding phonons) двух объемных компонент, усредненных в соответствии с (5), со щелью при k = n/d, обусловленной модуляцией массы. Две верхние ветви, которые можно было бы назвать сложенными оптическими фононами, нельзя описать как усредненные оптические зоны двух объемных компонент: верхняя ветвь почти плоская, и ее частота соответствует частоте объемного Si в точке Г, а более низкая ветвь довольно близка к частоте объемного Ge в точке Г. Таким образом, похоже, что для оптических фононов не происходит никакого усреднения. Подобный феномен обычно наблюдается для сверхрешеток, особенно для сверхрешеток с большой толщиной индивидуальных слоев. Это довольно наглядно иллюстрирует сделанное выше предположение о том, что оптические моды существуют в некотором интервале частот в одном из слоев, но не существуют в другом. Поэтому они называются модами с квантовым ограничением или квантованными модами.

Подобное сложение зоны Бриллюэна из-за увеличения периода сверхрешетки, определяемое числом элементарных ячеек в каждом слое, для сверхрешетки (GaAs)₈/(AlAs)₈ демонстрируется на рис.13, где также хорошо видно, как складываютя оптические ветви основных компонент сверхрешетки. Кроме того, на рисунке приведены атомные смещения для акустических движений и для оптических колебаний. Акустические колебания ведут себя также как и в объемном материале со средней скоростью звука, в то время как оптические колебания локализованы в каждом из слоев.

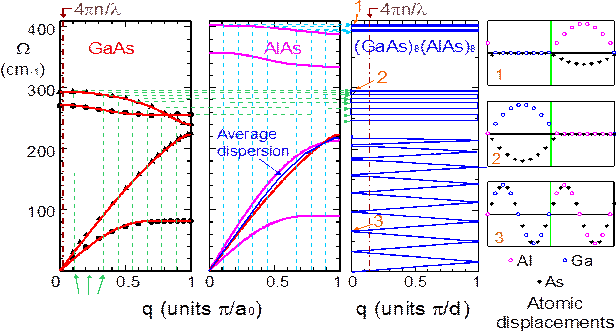
Рис. 13. Дисперсионные кривые (сплошные линии) для объемных GaAs (справа) и AlAs (посередине). Наблюдается сильное перекрытие частот их акустических мод, в отличие от оптических мод, для которых перекрытие отсутствует. Правая часть рисунка показывает сложенные акустические и оптические ветви в сверхрешетке (GaAs)₈ (AlAs)₈ и атомные смещения для точек 1, 2, и 3 в оптической ветви кристалла AlAs, в оптической ветви кристалла GaAs и в акустической сложенгной ветви сверхрешетки (AlAs)₈/(GaAs)₈.

Дисперсионные соотношения для сложенных акустических мод модно вычислить в макроскопическом приближении, соответствующему так называемом упругому пределу. Это справедливо для области частот, в которой дисперсия составляющих объемных материалов может считаться линейной. Для волн, распространяющихся вдоль оси роста, средняя скорость длинноволновых сложенных мод дается выражением (5). Для расчета полных дисперсионных соотношений, необходимо рассмотреть упругие волны в обеих средах, с одинаковой частотой ω. Компоненты волнового вектора q, перпендикулярного оси роста (q_x, q_y), должны быть равны в обоих средах, как и в случае электронных волновых функций. Компоненты же q вдоль z (q_z) должны изменяться при переходе из одной среды в другую, чтобы разным скоростям звука соответствовало одно и то же значение ω. Сверхрешетка как целое обладает трансляционной симметрией вдоль направления z с векторами трансляций, имеющими длину nd (п = ±1, ±2, ±3,...и т.д.. .). Поэтому смещение атомов в каждом слое можно выразить в форме блоховской волны.

Пусть в средах А и В существует по две волны с одинаковой частотой ω и волновы­ми векторами ±(q_x, q_y, q_zA), ±(q_x, q_y, q_zB), соответственно. Неизвестными являют­ся четыре амплитуды этих волн. Для произвольного направления распространения надо учесть все три возможных поляризации для акустических волн, т.е. всего имеет­ся 12 неизвестных амплитудных коэффициентов, которые надо найти из граничных условий. На интерфейсе должны быть непрерывны смещения (что дает три усло­вия), а также перпендикулярные к интерфейсу компоненты деформации, которые выражаются через градиенты смещений (три дополнительных условия). В результате получается секулярное уравнение размерности 12х12, что приводит к дисперсионным соотношениям для ω(q_x, q_y, k).

Секулярное уравнение в общем случае решается численными методами. В в случаях высокой симметрии (например, при q_x = q_y = 0 или q_y = k = 0) в сверхрешетке продольные и поперечные моды не смешиваются, и система уравнений упрощается.

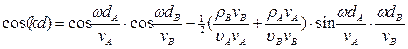(9)

где ρ_A, ρ_B,– плотности масс в слоях А и В.

Предыдущее уравнение можно переписать в слегка измененной форме:

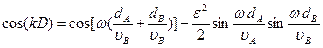
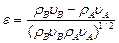(9a)

Отсюда видно, что при ε= 0 (в случае, когда акустические импедансы ρv обеих сред одинаковы), дисперсионное соотношение является просто соотношением для среды со средней скоростью звука, определяемой выражением (5).