Рівняння раціональної осі арки. Ядрові моменти
Ядровим моментом називається момент від усіх сил, узятих по одну сторону перетину, щодо крайньої точки ядра перетину.
При внецентровому стиску найбільша і найменша напруги виникають у крайніх точках поперечного перерізу і визначаються у виді
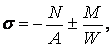
| (4.15) |
де А — площа поперечного перерізу; W — момент опору; N, M — повздовжня сила і згинальний момент у перетині відповідно.
При дії на арку рухомого навантаження для визначення найбільших нормальних напруг по формулі (4.15) одночасно доводиться завантажувати дві лінії впливу (N і M), що мають різні обриси, до того ж, одна з них — двохзначна. У зв'язку з цим вираз для 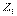 доцільно перетворити так, щоб формула (4.15) стала одночленною. Для цього розкладемо рівнодіючу лівих сил
доцільно перетворити так, щоб формула (4.15) стала одночленною. Для цього розкладемо рівнодіючу лівих сил 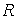 , прикладену в точці r перетину n – m (мал.4.7), на складові N і Q.
, прикладену в точці r перетину n – m (мал.4.7), на складові N і Q.
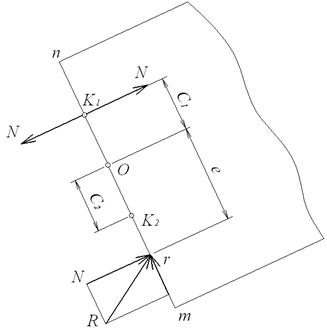
Рис.4.7. До перетворення виразу для 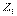
В одній із крайніх точок ядра перетину, наприклад, у верхній точці 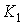 , прикладемо дві взаємно врівноважують сили N. У результаті цього в перетині будуть прикладені три сили N, які можна звести до пари сил з моментом
, прикладемо дві взаємно врівноважують сили N. У результаті цього в перетині будуть прикладені три сили N, які можна звести до пари сил з моментом 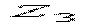 і подовжній силі N, що діє в крайній лівій ядровій точці. Тоді нормальна напруга в нижній точці m перетину визначається по формулі
і подовжній силі N, що діє в крайній лівій ядровій точці. Тоді нормальна напруга в нижній точці m перетину визначається по формулі
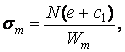
| (4.16) |
тому що від сили N, прикладеної у верхній ядровій точці, нормальна напруга в нижній точці m перетину дорівнює нулеві.
Добуток 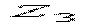 являє собою момент повздовжньої сили, прикладеної в точці r, щодо верхньої ядрової точки
являє собою момент повздовжньої сили, прикладеної в точці r, щодо верхньої ядрової точки 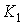 і називається ядровим моментом.
і називається ядровим моментом.
Відмінність ядрового моменту від звичайного згинаючого полягає в тому, що при його обчисленні потрібно множити ліві (або праві) сили на відстань до однієї з ядрових точок, а не до центра тяжіння перетину.
Аналогічно, нормальна напруга в точці n перетину визначається по формулі
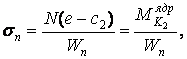
де 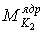 — момент зовнішніх лівих (або правих) сил щодо точки К2.
— момент зовнішніх лівих (або правих) сил щодо точки К2.
Ці формули є одночленними, що дозволяє більш просто вирішувати задачі, зв'язані з визначенням максимальних напруг у перетинах арки при дії на неї рухомого навантаження.
Раціональною віссю арки називається така вісь, при якій згинальний момент у всіх перетинах арки дорівнює нулеві.
Якщо вважати, що арка завантажена тільки вертикальними навантаженнями, то для цього необхідно і досить, щоб вертикальні ординати y усіх точок осі арки, відраховуванні від прямої (АВ), проведеної між опорами, були пропорційні відповідним ординатам «балкової» епюри моментів 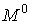 (мал.4.8), тобто в будь-якому перетині арки
(мал.4.8), тобто в будь-якому перетині арки
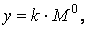
де y — вертикальні ординати точок, що лежать на осі балки; k — постійний коефіцієнт пропорційності; 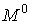 — ординати «балкової» епюри моментів.
— ординати «балкової» епюри моментів.
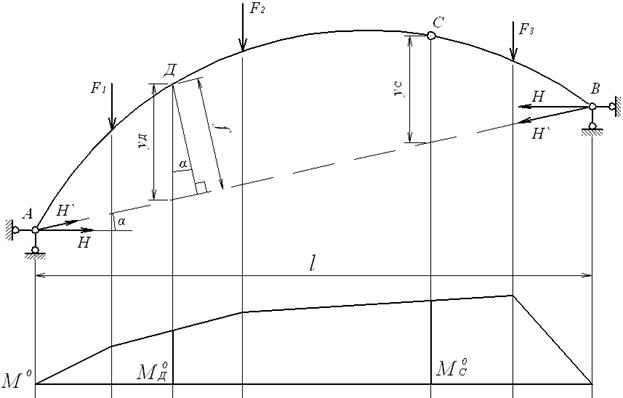
Рис.4.8. До визначення раціональної осі арки
У перетині D арки:

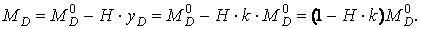
У шарнірі С:
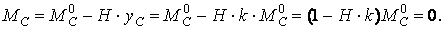
Тому що 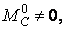 те
те 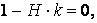
отже, 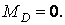
Дата добавления: 2015-01-29; просмотров: 1195;
