Социальное законодательство. Научно-практическое пособие
Задача К1. Вариант 39.
Точка В движется в плоскости ху (рис. К1, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями:
х = f1 (t), у = f2 (t), где х и у выражены в сантиметрах, t -в секундах.
Найти уравнение траектории точки; для момента времени t1 = 1с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Таблица К1
| Номер условия | |
| х = f1(t) | x = t – 4 |
| y = f2(t) | y = 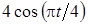
|
Решение
Движение точки задано координатным способом.
1. Найдем уравнение траектории, исключив из уравнений движения параметр t - время.
t = x + 4 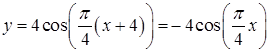 - косинусоида
- косинусоида
2. Находим положение точки при 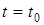 , подставляя это значение t в (1) и (2):
, подставляя это значение t в (1) и (2):
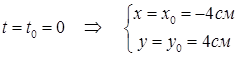
3. Находим положение точки при 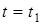 , подставляя это значение t в (1) и (2):
, подставляя это значение t в (1) и (2):
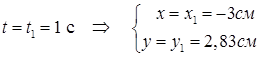
Указываем на рисунке точки 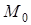 и
и 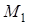 , учитывая масштаб координат.
, учитывая масштаб координат.
4. Найдем скорость точки. Из теории следует, что при координатном способе задания движения определяются сначала проекции скорости на оси координат. Используя (1) и (2) - уравнения движения точки - находим
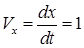 (3)
(3)
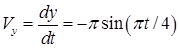 (4)
(4)
Модуль скорости 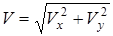 . (5)
. (5)
Подставляя сюда (3), (4), получим
При 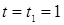 с :
с : 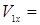 1см/с
1см/с  -2,22 см/с
-2,22 см/с
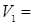 2,44 см/с (6)
2,44 см/с (6)
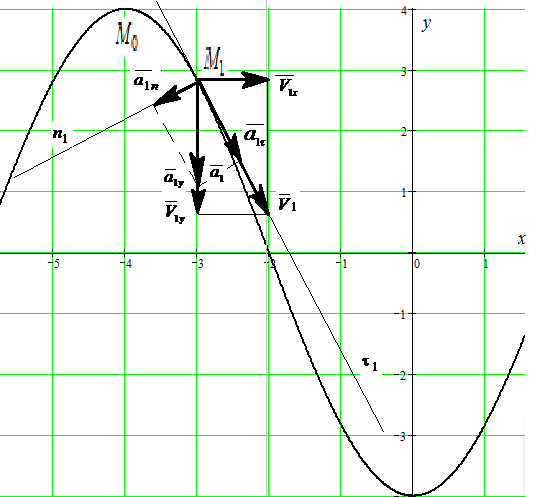
рис. К1.
Вектор  направлен по касательной к траектории в точке
направлен по касательной к траектории в точке 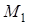 и показывает направление движения точки по траектории.
и показывает направление движения точки по траектории.
Удобно сейчас построить в точке 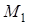 естественные оси: касательную
естественные оси: касательную 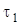 и главную нормаль
и главную нормаль 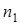 (они потребуются позже). Касательную
(они потребуются позже). Касательную 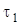 проводим вдоль
проводим вдоль  ; главную нормаль
; главную нормаль 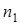 проводим перпендикулярно
проводим перпендикулярно 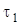 в плоскости рисунка и направляем к центру кривизны траектории в точке
в плоскости рисунка и направляем к центру кривизны траектории в точке 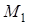 (в сторону вогнутости траектории).
(в сторону вогнутости траектории).
5. Находим ускорение точки, используя (3), (4):
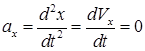 (7)
(7)
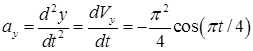 (8)
(8)
Модуль ускорения.
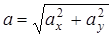 (9)
(9)
Подставляя в (7) - (9) 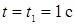 , найдем
, найдем
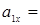 0 см/с2 ,
0 см/с2 , 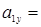 -1,74 см/с2,
-1,74 см/с2,
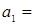 1,74 см/с2 (10)
1,74 см/с2 (10)
6. Находим касательное ускорение 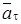 , характеризующее изменение модуля
, характеризующее изменение модуля 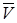 .
.
Касательное ускорение можно также найти, дифференцируя по времени равенство 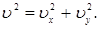 Получим
Получим
 , откуда следует
, откуда следует
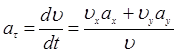
При 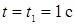
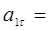
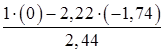 = 1,59 см/с2 (11)
= 1,59 см/с2 (11)
Нормальную составляющую 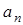 ускорения, характеризующую изменение направления
ускорения, характеризующую изменение направления 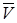 , можно найти по формуле
, можно найти по формуле
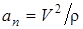 , (12)
, (12)
если 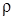 - радиус кривизны траектории заранее известен, или (учитывая, что,
- радиус кривизны траектории заранее известен, или (учитывая, что, 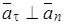 и, следовательно,
и, следовательно, 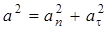 ) по формуле
) по формуле
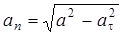 . (13)
. (13)
Так как в данной задаче радиус 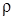 заранее неизвестен, то используем (13). Подставляя (10), (11) в (13), получим
заранее неизвестен, то используем (13). Подставляя (10), (11) в (13), получим
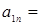
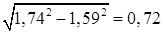 см/с2 (14)
см/с2 (14)
Найдем радиус кривизны 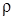 , используя (12), откуда следует, что
, используя (12), откуда следует, что 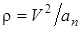 . Подставляя в последнее соотношение
. Подставляя в последнее соотношение 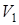 и
и 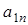 из (6) и (14), получим радиус кривизны траектории в точке
из (6) и (14), получим радиус кривизны траектории в точке 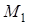 :
: 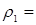
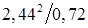 = 8,29 см
= 8,29 см
Объединяя полученные результаты, запишем ответ:
1. траектория точки - 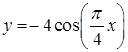
2. 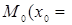 -4 см,
-4 см, 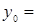 4см
4см 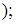
3. 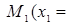 -3 см
-3 см 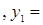 2,83 см
2,83 см 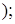
4. 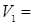 2,44 см/с;
2,44 см/с;
5. 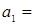 1,74 см/с2 ;
1,74 см/с2 ;
6. 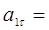 1,59 см/с2 ;
1,59 см/с2 ; 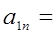 0,72 см/с2;
0,72 см/с2;
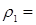 8,29 см
8,29 см
Задача К1б. Вариант 39.
Точка В движется по дуге окружности радиуса R = 2 м по закону
S = f (t) = -2 cos(πt/6) ( s – в метрах, t – в секундах), где S= 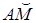 - расстояние от точки до некоторого начала А, измеренное вдоль дуги окружности (естественный способ задания движения точки). Для момента времени t1 = 1с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения.
- расстояние от точки до некоторого начала А, измеренное вдоль дуги окружности (естественный способ задания движения точки). Для момента времени t1 = 1с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения.
Изобразить на рисунке векторы 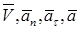 , считая, что точка в этот момент находится в положении М, а положительное направление отсчета s – от А к М. Установить характер движения точки при t1 = 1с (ускоренное или замедленное).
, считая, что точка в этот момент находится в положении М, а положительное направление отсчета s – от А к М. Установить характер движения точки при t1 = 1с (ускоренное или замедленное).
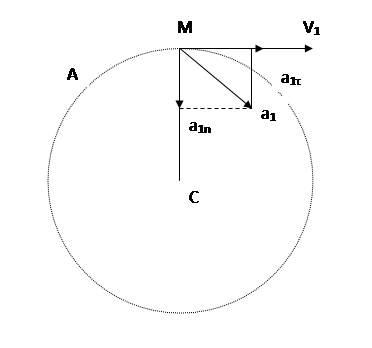
Решение:
Определяем скорость точки:
V = 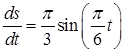
При t1 = 1с получим V1 = 0,52м/с
Ускорение находим по его касательной и нормальной составляющим:
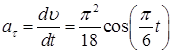
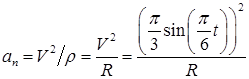
При t1 = 1с получим, учитывая,
что R= 2 м,
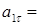 0,14м/с2
0,14м/с2
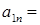 0,47 м/с2
0,47 м/с2
Тогда ускорение точки при t1 = 1с будет
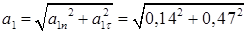 =0,49 м/с2
=0,49 м/с2
Ответ: V1 = 0,52 м/с
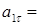 0,14 м/с2
0,14 м/с2
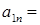 0,49 м/с2
0,49 м/с2
Движение точки ускоренное,
т.к. V1>0, а 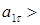 0.
0.
Задача К2. Вариант 39.
Механизм состоит из ступенчатых колес 1-3, находящихся в зацеплении или связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес (рис. К2). Радиусы ступеней колес равны соответственно: у колеса 1 – r1 = 2 см, R1 = 4 см, у колеса 2 – r2 = 6 см, R2 = 8 см, у колеса 3 – r3 = 12 см, R3 = 16 см. На ободах колес расположены ( в произвольном месте обода) точки А, В и С. Таблица К2.
| Номер условия | Дано | Найти | |
| скорости | ускорения | ||
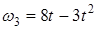
| 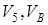
| 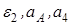
|
Определить в момент времени t1 = 2с указанные в таблице в столбцах «Найти» скорости и ускорения соответствующих точек и тел.
Решение: вращательное движение колеса 3 преобразуется в поступательное и во вращательное движение колеса 2 через трос, в свою очередь вращательное движение колеса 2 преобразуется в движение рейки 4, Также вращательное движение колеса 3 преобразуется вращательное движение колеса 1, которое преобразуется в поступательное движение груза 5.
По условию задачи, закон движения рейки
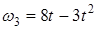 (1)
(1)
Из (1) находим скорость рейки 4.
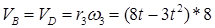 (трос) (1)
(трос) (1)
тогда 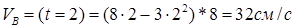
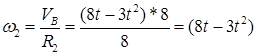
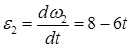 , тогда
, тогда 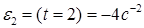 (2)
(2)
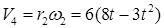 ,
,
отсюда 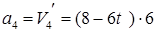 , тогда
, тогда 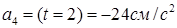 (3)
(3)
Составим пропорцию для точки С: 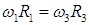
, тогда 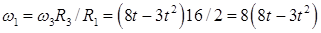 (7)
(7)
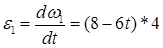 , тогда
, тогда 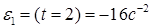 (9)
(9)
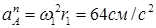 ; вектор
; вектор 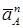 направлен к оси вращения.
направлен к оси вращения.
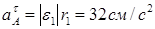 ; Вектор
; Вектор 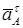 направлен перпендикулярно оси вращения.
направлен перпендикулярно оси вращения.
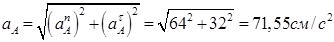
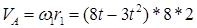 , тогда
, тогда 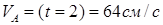 (10)
(10)
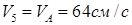 (11)
(11)
Ответ: 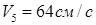 ,
, 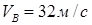 ,
, 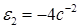 ,
,  ,
, 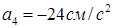
Задача К4. Вариант 39.
Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна Е(Рис. К4), соединенных друг с другом и с неподвижными опорами шарнирами О1, О2; точка D находится на середине стержня АВ. Длины стержня равны соответственно: l1 = 0,4 м, l2= 1,2 м, l3 = 1,4 м, l4 = 0,6 м. Положение механизма определяется углами α, β, γ, φ, θ.
Таблица К4.
| Номер условия | Углы, град | Дано | Найти | ||||||||
| a | b | g | j | q | w1, 1/c | w4, 1/c | V точек | w звена | a точки | e звена | |
| - | A, E | DE | A | AB |
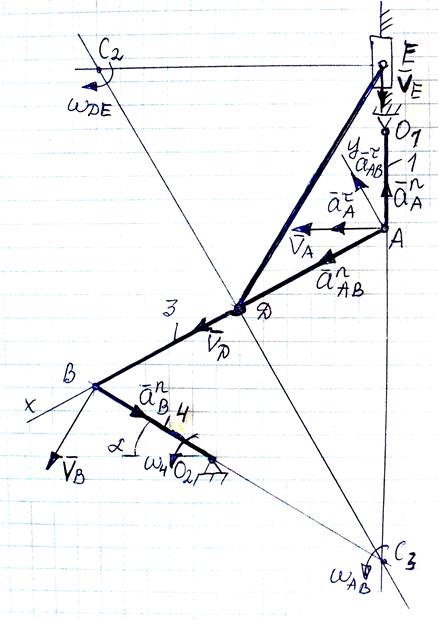
Рис. К4.
Решение: 1. Строим положение механизма в соответствии с заданными углами и длинами стержней (Рис. К4; на этом рисунке в процессе решения задачи изображаем все векторы скоростей).
2. Определяем VА. Точка А принадлежит стержню 1, совершающему плоскопараллельное движение. Чтобы найти 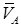 , нужно знать направление
, нужно знать направление 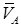 и скорость другой точки звена 3. Такой точкой является точка В, принадлежащая еще звену 4(звено вращается)
и скорость другой точки звена 3. Такой точкой является точка В, принадлежащая еще звену 4(звено вращается) 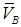 направлена в сторону поворота стержня 4.
направлена в сторону поворота стержня 4.
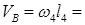 8·0,6 = 4,8 м/с;
8·0,6 = 4,8 м/с; 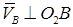 (1)
(1)
Направление 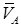 найдем, учитывая, что точка А принадлежит одновременно стержню 1 и, следовательно,
найдем, учитывая, что точка А принадлежит одновременно стержню 1 и, следовательно,  . Теперь, зная
. Теперь, зная 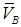 и направление
и направление 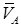 , воспользуемся теоремой о проекциях скоростей двух точек тела (стержня 3) на одну прямую, соединяющую эти точки (прямая АВ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор
, воспользуемся теоремой о проекциях скоростей двух точек тела (стержня 3) на одну прямую, соединяющую эти точки (прямая АВ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор 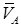 (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
(проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
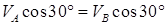 и
и 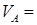 4,8 м/с (2)
4,8 м/с (2)
3. Определяем 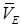 . Точка Е принадлежит стержню 2, совершающему плоскопараллельное движение. Следовательно, по аналогии с предыдущим, чтобы определить
. Точка Е принадлежит стержню 2, совершающему плоскопараллельное движение. Следовательно, по аналогии с предыдущим, чтобы определить 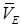 , надо сначала найти скорость точки D, принадлежащей одновременно стержню 2. Для этого, зная
, надо сначала найти скорость точки D, принадлежащей одновременно стержню 2. Для этого, зная 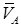 и
и 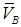 , строим мгновенный центр скоростей (МЦС) стержня АВ; это точка С3, лежащая на пересечении перпендикуляров к
, строим мгновенный центр скоростей (МЦС) стержня АВ; это точка С3, лежащая на пересечении перпендикуляров к 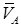 и
и 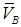 , восстановленных из точек А и В. По направлению вектора
, восстановленных из точек А и В. По направлению вектора 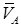 определяем направление мгновенного поворота стержня 3 вокруг МЦС С3. Вектор
определяем направление мгновенного поворота стержня 3 вокруг МЦС С3. Вектор 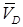 перпендикулярен отрезку С3D, соединяющему точки D и С3, и направлен в сторону мгновенного поворота тела. Величину
перпендикулярен отрезку С3D, соединяющему точки D и С3, и направлен в сторону мгновенного поворота тела. Величину 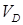 найдем из пропорции
найдем из пропорции
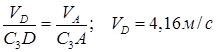 ;
; 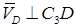 (3)
(3)
Так как точка Е одновременно принадлежит ползуну Е, движущемуся по направляющим ползуна. Теперь, зная 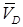 и направление
и направление 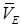 , воспользуемся теоремой о проекциях скоростей двух точек тела (стержня 2) на одну прямую, соединяющую эти точки (прямая ED). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор
, воспользуемся теоремой о проекциях скоростей двух точек тела (стержня 2) на одну прямую, соединяющую эти точки (прямая ED). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор 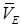 (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
(проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
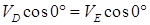 и
и  4,16 м/с (4)
4,16 м/с (4)
4. Определяем ωDE. Для этого, зная 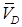 и
и 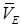 , строим мгновенный центр скоростей (МЦС) стержня DE; это точка С2, лежащая на пересечении перпендикуляров к
, строим мгновенный центр скоростей (МЦС) стержня DE; это точка С2, лежащая на пересечении перпендикуляров к 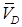 и
и 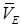 , восстановленных из точек D и E. По направлению вектора
, восстановленных из точек D и E. По направлению вектора 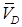 определяем направление мгновенного поворота стержня 2 вокруг МЦС С2.
определяем направление мгновенного поворота стержня 2 вокруг МЦС С2.
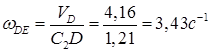 (5)
(5)
5. Определяем аА. Точка А принадлежит стержню 3. Чтобы найти 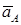 , надо знать траекторию точки А и ускорение какой-нибудь другой точки стержня 3. Такой точкой является точка В, принадлежащая звену 4. Следовательно,
, надо знать траекторию точки А и ускорение какой-нибудь другой точки стержня 3. Такой точкой является точка В, принадлежащая звену 4. Следовательно, 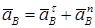 , где численно
, где численно
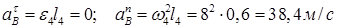 (6)
(6)
Вектор 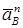 направлен вдоль ВО2; изображаем этот вектор на чертеже. Так как точка А принадлежит одновременно стержню 1, то вектор
направлен вдоль ВО2; изображаем этот вектор на чертеже. Так как точка А принадлежит одновременно стержню 1, то вектор 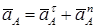 . Вектор
. Вектор 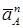 направлен вдоль АО1, а вектор
направлен вдоль АО1, а вектор 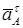 - перпендикулярно АО1, ; изображаем эти векторы на чертеже.
- перпендикулярно АО1, ; изображаем эти векторы на чертеже.
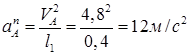 (7)
(7)
Для определения 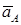 воспользуемся равенством ( В – полюс):
воспользуемся равенством ( В – полюс):
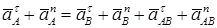 (8)
(8)
Изображаем на чертеже в точке А векторы: 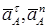 ( переносное ускорение точки А),
( переносное ускорение точки А), 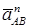 (вдоль АВ от А к В) и
(вдоль АВ от А к В) и 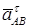 ( в любую сторону перпендикулярно АВ); численно
( в любую сторону перпендикулярно АВ); численно  .
.
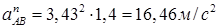 (9)
(9)
Таким образом, у величин, входящих в равенство (8), неизвестны только числовые значения 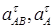 ; их можно найти, проектируя обе части равенства АВ (ось х), перпендикулярное неизвестному вектору
; их можно найти, проектируя обе части равенства АВ (ось х), перпендикулярное неизвестному вектору 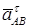 . Тогда получаем
. Тогда получаем
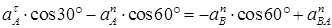
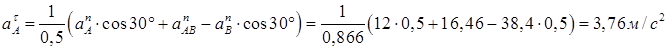 (10)
(10)
Отсюда
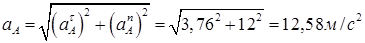 (11)
(11)
6. Определяем εАВ. Чтобы найти εАВ, сначала определим 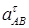 . Для этого обе части равенства (8) проектируем на направление, перпендикулярное АВ (ось у); получаем:
. Для этого обе части равенства (8) проектируем на направление, перпендикулярное АВ (ось у); получаем:
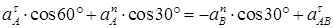 (12)
(12)
Подставив в равенство (12) числовые значения всех величин, найдем
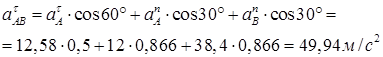
Знак указывает, что направление 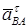 выбрано верно.
выбрано верно.
Из равенства  получим
получим 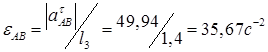
Ответ: 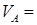 4,8 м/с;
4,8 м/с;  4,16 м/с;
4,16 м/с;  ;
; 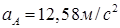 ;
; 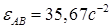
Социальное законодательство. Научно-практическое пособие
Дата добавления: 2015-01-09; просмотров: 1743;
