Системно-информационно-синергетический подход к оценке здоровья

Развиваемый нами системно-информационно-синергетический подход к оценке здоровья основывается на общей теории систем [Богданов А.А., 1925, Берталанфи Л., 1969, Виннер Н., 1984, Блауберг И.В.. Юдин Ю.Г., 1973], теории функциональных систем П.К.Анохина [1970, 1978, 1980] и его школы [Судаков К.В., 1993, 1997; Фудин Н.А., 1983; Зилов В.Г., 2004], те­ории информации [Шмальгаузен И.И., 1968, Виннер Н., 1958, Колмогоров А.Н., 1987], теории хаоса и синергетики [Пригожин И., 1985; Хакен Г., 2000; В.М. Еськов 2004 - 2008 и др].

Как из­вестно, системное исследование исходит из принципа целостности, согласно которому объект рассматривается как относительно обо­собленная система, свойства которой не сводимы к свойствам ее частей. Только путь от целого к частям приводит к пониманию природы элементов и характера их взаимодействия.

Согласно взглядам академика И.И. Шмальгаузена [1968]., информацион­ный подход к построению теоретической биологии обеспечивает ту теоретическую основу, которая позволяет объединить и объяснить все колоссальное разнообразие биологических фактов. И сама эволюция человека и человеческого общества протекает строго в соответствии с принципом уменьшения энтропии, усилением самоорганизации и накопления информации.

По К. Шен­нону информация, которую содержит событие (предмет, состояние) у о событии (предмете, состоянии) х, равна:

I (x, y) = log 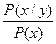, где (1)

P (x) - вероятность события х до наступления события у (безуслов­ная вероятность; P (x/y) - вероятность события х при условии наступления события у (условная вероятность).

Под событиями х и у можно понимать стимул и реакцию, вход и выход, значения двух различных переменных, характеризующих состояние системы [Голицин Г.А., Петров В.М., 1990]. Средняя взаимная информация между двумя множествами собы­тий, двумя переменными x и y определяется по формуле:

I (x, y) = H (x) – H (x/y), где (2)

Н (x) - безусловная энтропия, а Н (x/y) - условная энтропия.

Чем больше взаимная информация, тем меньше условная энтропия. При этом речь идет не о количестве информации вообще, а о ценной информации, т.е. той, которая помогает достижению цели (Д.С. Чернавский, 2009). Эк­стремальный принцип, определяющий многие формы поведения живых организмов, носит название «принцип максимума информации». Для достижения полезного результата организм должен обеспечить максимум взаимной информации между условиями среды и реакциями:

I (x,y) = max , где (3)

X - стимул, условия внешней среды, воздействующие на организм; У- реакция организма на стимул с целью достижения полезного результата.

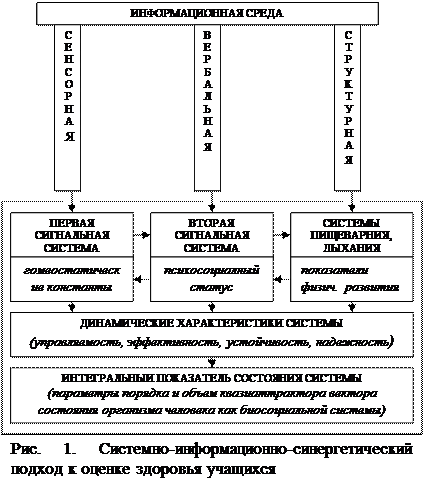
Все многообразие информации (стимулов), воздействующей на организм, может быть сведено к трем потокам: сенсор­ному, воспринимаемому органами чувств через первую сигнальную систему; вербальному (устное или письменное слово) - через вторую сигнальную систему; структурному (компоненты пищи и вдыхаемого воздуха), поступающему через желудочно-кишечный тракт и дыхательную систему [Брехман И.И., 1990]. Таким образом, в организме в единстве действуют системы, адекватные управляющими сигналами которых являются вещественные (концентрация химических веществ и гормонов в крови), энергетические (свет, звук) и информационные (смысл слова, предложения, команды).

В этой связи, нами выделяются три блока воспринимающие информацию (рис. 1). Их выделение, по сути, соот­ветствует эволюционно выработанным способам, посредством которых может реализоваться принцип максимума информации. При помощи первой сигнальной системы организм стремится приспособиться к большому разнообразию условий внешней среды Н(x), сохранив при этом постоянство (гомеостазис), т.е. минимальное разнообразие результатов Н(x/y).

За счет второй сигнальной системы организм стремится уве­личить безусловное разнообразие реакций Н(y), поскольку это его арсенал вборьбе за результат, и, в то же вре­мя, уменьшить разнообразие условное Н(x/y), т.е. неоднозначность, неточность ответов на конкретный стимул. Посредством питания и дыхания осуществляется наиболее тесный и постоянный контакт человека с природой. Естественно предположить, что эволюционно наиболее древ­нее химическое информационное взаимодействие организмов со средой привело к созданию специальной знаковой системы, позво­ляющей отличить одну химическую структуру от другой по принципу комплементарности [Брехман И.И., 1990]. Но комплементарность в дан­ном случае является еще одним способом реализации принципа максимума информации, т.к., согласно формуле 1, информация тем больше, чем выше точность сообщения.

Считается, что все три потока информации соединяются на некотором химическим уровне [Брехман И.И., Кубланов М.Г., 1983]. Организм имеет определенную пропускную способность восприятия информации и возможность ее перераспределения внутри этого триединого потока. К примеру, в функционировании сенсорных систем, за счет саморегуляторных механизмов (торможение, доминирующая мотивация и т.д.), постоянно проявляется стремление извлечь как можно больше полезной информации и не допустить перегрузки центральной нервной системы [Судаков К.В., 1993]. Открытый позже [1997] К.В. Судаковым принцип информационных связей между элементами функциональных систем определяет дальнейший путь развития теоретических представлений о функциональных системах как информационных системах. К сожалению, современные мето­ды исследований не позволяют пока заглянуть в этот информаци­онный "котел", поэтому мы будем пользоваться общепринятыми в настоящее время показателями.

Согласно теории функциональных систем П.К.Анохина, цент­ральным элементом системы является конечный полезный эффект, обеспечивающий ее нормальные функции в биологическом и социальном планах. В нашем случае он будет складываться, во-первых, из ре­зультатов деятельности трех блоков, воспринимающих информацию. Результатом деятельности блока, вос­принимающего структурную информацию, являются биологический возраст, соматотип, уровень физического развития и физической подготовленности ребенка, показатели внешнего дыхания.

Конечный полезный эффект деятельности первой сигнальной системы выражается в поддержании постоянства внут­ренней среды организма. С позиций теории управле­ния гомеостаз обеспечивается за счет управления внутренними параметрами системы на основе переработки поступающей на ее вход информации о состоянии внешней среды. Если представить организм, как кибернетическую систему, состоящую из управляюще­го (центральная и вегетативная нервная системы) и управляемого (опорно-двигательный аппарат и внутренние органы) элементов, то согласующим звеном между ними является аппарат кровообращения [Баевский Р.М., 1976]. Поэтому на основе реакции этой системы может бать да­на оценка гомеостазу. Математический анализ ритма сердца явля­ется, на сегодняшний день, наиболее адекватным количественным способом такой оценки.

Для второй сигнальной системы таким результатом будет психосоциальный статус человека. Для школьника он означает, во-первых, его способность к выполнению своих социальных функций и, во-вторых, соответствующий психоэмоци­ональный уровень. Способность школьника к выполнению социаль­ных функций в конечном итоге выражается в успешности освоения им общеобразовательных дисциплин, наличии необходимых знаний, умений, навыков, компетенций и показателях личностного развития.

Перечисленные па­раметры характеризуют систему, так сказать, в статике и ничего не говорят о ее динамических характеристиках. Система может считаться совершенной только в том случае, если она обладает рядом функциональных свойств. К ним, прежде всего, относятся: управляемость, эффективность, устойчивость, надежность.

Свойством управляемости обладают только определенным об­разом организованные системы, т.е. обладающие целесообразным составом и связями между элементами. Управление тесно связано с гомеостазом и адаптивностью, позволяющими системе самооптимизировать свое поведение и структуру при действии случайных факторов различного происхождения. По соотношению различных контуров управле­ния можно определить тип регуляции, а ее качество удается выя­вить при анализе переходных процессов в системе в ответ на от­клонение регулируемого параметра. Показателем эффективности является величина, выражающая степень приспособленности системы к выполнению поставленных перед нею задач. Количественным показателем эффективности мышечной деятельности принято считать соотношение полезной работы к общим затратам энергии или пульсовую стоимость нагрузки. При оценке пси­хической деятельности обычно вычисляют отношение правильных решений к общему числу предъявленных задач или числу тестов, решаемых за определенное время. Система должна обладать определенной устойчивостью функ­ционирования, т.е. способностью сохранять требуемые свойства в условиях воздействия возмущений. Она может быть определена зоной сохранения максимальных значений эффективности по мере нарастания прост­ранственно-временной нагрузки. Для характеристики надежности на практике часто определяют функциональные ре­зервы организма, представляющие собой разницу между максималь­ными значениями функции и минимальными в состоянии физиологи­ческого покоя.

Наибольшие трудности связаны с количественным определением интегрального показателя состояния учащегося, как сложноорганизованной биосоциальной системы, т.к. для этого необходимо сформулировать «решающее правило», являющееся основой любой классификации. В теоретическом плане общим ориентиром для научного поиска в этом направлении служит синергология, которая в настоящее время рассматривается как основа междисциплинарного синтеза знаний [Пригожин И., 1985, 1986; Хакен Г., 2000 и др.]. Развитие и поведение функциональных систем организма на различных этапах школьного онтогенеза вполне можно отнести к синергетическому, так как оно проявляет все свойства открытой самоорганизующейся системы: сложность (сложность организма человека, особенно когда он рассматривается как биосоциальная система); открытость (обмен веществом, энергией, структурной, сенсорной и вербальной информацией с окружающей средой); нелинейность (нелинейность развития организма в онтогенезе, наличие критических, сенситивных периодов); стохастичность (многовариантность и вероятностный характер развития организма под влиянием сложного комплекса природно-климатических и социальных факторов); неустойчивость (возможность изменения траектории развития организма под воздействием внешней среды); неравновестность (например, стремление к сохранению гомеостаза); диссипативность (наличие процессов, полная энергия которых переходит в другие виды энергии); способность к самоорганизации (усложнение структуры системы, когда внешнее воздействие превосходит некоторое критическое значение, например, «тренирующий стресс», саморазвитие культуры здоровья и т.д.).

Долгое время использование этого направления сдерживалось отсутствием общих и доступных методов идентификации степени различий между хаосом и стохастикой, единых методических подходов в теории идентификации моделей, общих принципов построения таких моделей. Однако в последние годы ситуация изменилась. Впервые дано обоснование единства детерминисткого, стохастического и хаотического (синергетического) подходов, показана их гносеологическая связь. Используя такое гносеологическое единство, ряду авторов удалось описать и идентифицировать уникальные параметры биосистем – размеры квазиаттракторов вектора состояний организма человека, степень синергизма, интервалы устойчивости биосистем на примере функциональных систем организма человека в фазовом пространстве состояний [В.М. Еськов, 2005, 2006, 2007; А.А. Хадарцев, В.М. Еськов, 2005].

Синергетика не использует традиционное разложение объекта на составляющие элементы, а подходят к нему с позиций системного анализа и синтеза. Любая система описывается вектором состояния системы в m- мерном фазовом пространстве состояний с параметрами реальных аттракторов движения системы. Системный анализ и синтез, в этой связи, сводится к отысканию параметров порядка (наиболее важных динамических переменных, описывающих процесс) и русел (законов, по которым развивается система), а также областей бифуркаций и джокеров, когда система резко меняет свои параметры и приобретает принципиально новые свойства.

Состояние детей на определенном этапе школьного онтогенеза описывается точкой в m – мерном пространстве, координаты которого образуют диагностические признаки 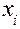(здесь i = 1,2,….m, где m – общее число диагностических признаков). Чтобы получить реальный портрет изучаемого объекта, число таких диагностических признаков должно быть либо максимальным, что трудно достижимо с практической точки зрения. Либо отвечать системному принципу необходимости и достаточности, т.е. быть строго аргументировано. В нашем случае такое обоснование осуществлено с позиций теорий информации и систем.

Таким образом, диагностические признаки 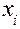представляют параметры порядка вектора состояния человека 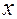= ( 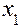, ,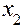.. 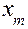) 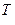в m-мерном фазовом пространстве состояний. Полученные значения (компартменты) 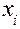по каждому 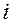-му признаку переносятся в фазовое пространство состояний на базе ЭВМ. В результате для каждой группы детей определенного возраста получается набор точек в виде «облака», которые имеют свои координаты на всех осях 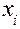( 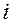= 1,2,….m) и которые для каждой координаты 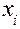имеют свои (для каждой возрастной группы) крайние значения (границы отрезков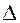 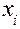на осях 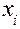). Они обозначаются как грани и содержат левую крайнюю точку 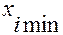и правую крайнюю точку 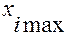, т.е.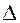 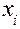= = 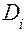( 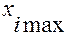- 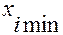). Полученные грани 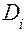характеризуют степень флуктуации вектора состояния по каждой координате 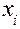, а вектор 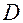= ( 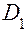, ,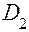… ) 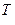характеризуют общую степень флуктуации вектора состояния в фазовом пространстве состояний для детей определенной возрастной группы. Полученные значения всех граней 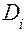в фазовом пространстве состояний образуют некоторый m-мерный параллелепипед, внутри которого движется вектор состояния в фазовом пространстве состояний для данной группы детей. 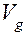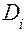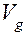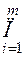Для этой группы рассчитывается объем m-мерного параллелепипеда как произведение всех граней: = 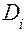, внутри которого находится квазиаттрактор движения вектора состояния в фазовом пространстве состояний, и который приблизительно будет представлять объем этого квазиаттрактора. Если необходимо сравнить различные возрастные группы, производится расчет 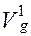объема квазиаттрактора предыдущей и 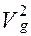последующей возрастной группы и рассчитывается изменение этих объемов ( = - ).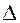

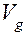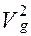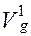Одновременно производится расчет координат вектора 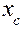= ( 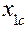, ,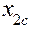.. ) 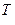центра 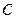m-мерного параллелепипеда, представляющего центр квазиаттрактора движения вектора состояния по формуле: 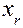= 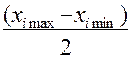. Наконец, производится расчет показателя асимметрии 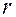, который равен расстоянию между центром 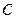квазиаттрактора движения вектора состояния и центром «масс», т.е. средневзвешенным (центр всех статистических математических ожиданий) = ( 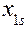, ,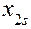… 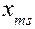) 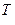по формуле: 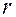= 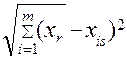. Чем больше 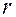, тем дальше стохастический центр отстоит от хаотического (т.е. центра квазиаттрактора).

Для определения значимости каждого 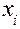компонента вектора состояния для всего вектора 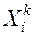вводили параметр 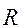, показывающий степень изменения объема квазиаттракторов для k-го кластера данных до и после уменьшения размерности фазового пространства. В исходном приближении = ( 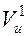,- 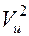)/ 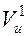. После исключения поочередно каждой из 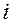координат вектора 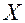(например, для двухкластерных систем) вычисляются вторые приближения параметров 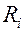= ( 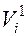- 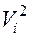)/ 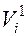. Таким образом, получаем вектор 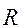= ( …., 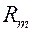) 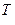, т.е. вектор значений, по которым можно определить уменьшилась или увеличилась относительная величина квазиатракторов 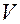при изменении размерности фазового пространства. При уменьшении относительных размеров 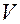, анализируются параметры системы и на основе их изменчивости делается заключение о значимости каждого 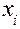компонента вектора состояния для всего вектора 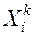= ( 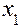, ,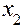.. 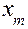) 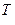, т.е. для 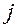-го испытуемых из 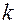-го массива данных.

Следует особо отметить высокую чувствительность развиваемого подхода в сравнении с традиционным (среднестатистическим). Дело в том, что традиционные подходы совершенно не чувствительны к отдельным «выбросам» компонент вектора состояния организма человека. Более того, в статистике они иногда просто отбрасываются (правило трех сигм). С позиций же теории хаоса и синергетики именно они увеличивают суммарные объемы аттракторов, а, значит, позволяют на более ранней стадии увидеть изменения координат центров аттракторов движения в фазовом пространстве состояний вектора состояния организма человека.

Таким образом, предлагаемый нами системно-информационно-синергетический подход к оценке здоровья школьников с учетом принципа необходимости и достаточности позволяет обоснованно подбирать показатели, характеризующие состояние здоровья человека как сложноорганизованной биосоциальной системы.