Парной линейной корреляции

Простейшей системой корреляционной связи является линейная связь между двумя признаками - парная линейная корреляция.

Практическое значение ее в том, что есть системы, в которых среди всех факторов, влияющих на результативный признак, выделяется один важнейший фактор, который в основном определяет вариацию результативного признака. Измерение парных корреляций составляет необходимый этап в изучении сложных, многофакторных связей. Есть такие системы связей, при изучении которых следует предпочесть парную корреляцию. Внимание к линейным связям объясняется ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные формы связей для выполнения расчетов преобразуются в линейную форму.

Уравнение парной линейной корреляционной связи называется уравнением парной регрессии и имеет вид:

у = а + bх, (8.4)

где у - среднее значение результативного признака> при определенном значении факторного признака х;

а - свободный член уравнения;

b - коэффициент регрессии, измеряющий среднее отношение отклонения результативного признака от его средней величины к отклонению факторного признака от его средней величины на одну единицу его измерения - вариация у, приходящаяся на единицу вариации х.

Что касается термина регрессия, его происхождение таково: создатели корреляционного анализа Ф. Гальтон (1822 - 1911) и К. Пирсон (1857 - 1936) интересовались связью между ростом отцов и их сыновей. Ф. Гальтон изучил более 200 семей и обнаружил, что в группе семей с высокорослыми отцами сыновья в среднем ниже ростом, чем их отцы, а в группе семей с низкорослыми отцами сыновья в среднем выше отцов. Таким образом, отклонение роста от средней в следующем поколении уменьшается -регрессирует. Причина в том, что на рост сыновей влияет не только рост отцов, но и рост матерей и много других факторов развития ребенка, и эти факторы, случайно направленные как в сторону увеличения, так и снижения роста, приближают рост сыновей к среднему росту. В целом же вариация роста, конечно, не уменьшается, а в наше время «акселерации» сам средний рост увеличивается из поколения в поколение.

Уравнение (8.4) определяется по данным о значениях признаков х и у в изучаемой совокупности, состоящей из п единиц. Параметры уравнения а и b находятся методом наименьших квадратов (МНК).

Исходное условие МНК для прямой линии имеет вид:

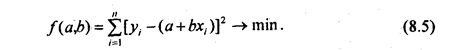
Для отыскания значений параметров а ч b, при которых f(a,b) принимает минимальное значение, частные производные функции приравниваем нулю и преобразуем получаемые уравнения, которые называются нормальными уравнениями МНК для прямой:

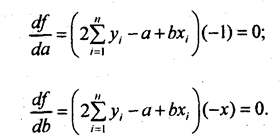
Отсюда система нормальных уравнений имеет вид:

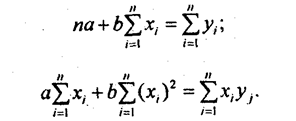
Нормальные уравнения МНК для прямой линии регрессии являются системой двух уравнений с двумя неизвестными а и b. Все остальные величины, входящие в систему, определяются по исходной информации. Таким образом, однозначно вычисляются при решении этой системы уравнений оба параметра уравнения линейной регрессии.

Если первое нормальное уравнение разделить на п, получим:

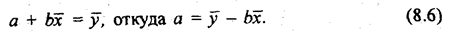
По уравнению (8.6) обычно на практике вычисляется свободный член уравнения регрессии а. Параметр b вычисляется по преобразованной формуле, которую можно вывести, решая систему нормальных уравнений относительно b:

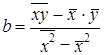. (8.7)

Так как знаменатель этого выражения есть не что иное, как дисперсия признака х, т. е. ст²^, то можно записать формулу коэффициента регрессии в виде:

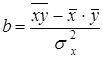(8-8)

Подставив в (8.8) выражение для s²_x, получим:

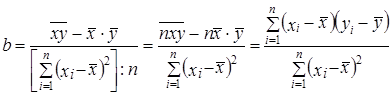. (8.9)

Параметры уравнения регрессии можно вычислить через определители:

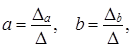(8.10)

где D - определитель системы;

D_a - частный определитель, получаемый в результате замены коэффициентов при а свободными членами из правой части системы уравнений;

D_b - частный определитель, получаемый в результате замены коэффициентов при b свободными членами из правой части системы уравнений.

Формулы (8.10) соответствуют самому общему подходу к определению параметров уравнения регрессии и могут применяться в случае как парной, так и множественной регрессии.

Применение одной из формул (8.7), (8.8) или (8.9) зависит от характера данных и наличия уже вычисленных на предыдущих этапах анализа показателей. Если были вычислены x̅, y̅, s_x, s_y, то проще применить формулу (8.7) или (8.8). Если расчет параметров уравнения корреляционной связи ведется исходя из первичных данных х_i, у_i, то удобнее формула (8.9). Особенно существенно она сокращает объем вычислений при слабой вариации признаков, ибо тогда отклонения их индивидуальных значений от средних величин на порядок или два меньше самих индивидуальных и средних величин. Кроме того, формула (8.9) явно выражает указанную в п. 8.1 особенность корреляционного анализа связей: параметры корреляции зависят не от уровней признаков, а только от их отклонений от средних значений.

Если значение признака увеличить в 10 раз, корреляция не изменится, также не изменятся параметры корреляции, кроме свободного члена, если ко всем значениям каждого признака прибавить постоянное число.

Коэффициент парной линейной регрессии, обозначенный Ь, имеет смысл показателя силы связи между вариацией факторного признака х и вариацией результативного признака у. Он измеряет среднее по совокупности отклонение у от его средней величины при отклонении признака х от своей средней величины на принятую единицу измерения.

Например, по данным табл. 8.1 при отклонении затрат на 1 корову от средней величины на 1 руб. надой молока на корову отклоняется от своего среднего значения на 3,47 кг в среднем по совокупности. При отклонении фактора на х̅_i - х̅ результативный признак отклоняется в среднем на у̅_i - у̅.

Теснота парной линейной корреляционной связи, как и любой другой показатель, может быть измерена корреляционным отношением h. Кроме того, при линейной форме уравнения применяется другой показатель тесноты связи - коэффициент корреляции r_xy. Этот показатель представляет собой стандартизованный коэффициент регрессии, т. е. коэффициент, выраженный не в абсолютных единицах измерения признаков, а в долях среднего квадратического отклонения результативного признака:

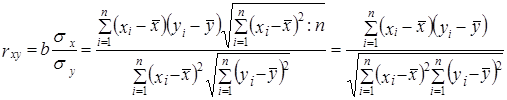. (8.11

Коэффициент корреляции был предложен английским статистиком и философом Карлом Пирсоном (1857 - 1936). Его интерпретация такова: отклонение признака-фактора от его среднего значения на величину своего среднего квадратического отклонения в среднем по совокупности приводит к отклонению признака-результата от своего среднего значения на r_xy его среднего квадратического отклонения.

В отличие от коэффициента регрессии b коэффициент корреляции не зависит от принятых единиц измерения признаков, а стало быть, он сравним для любых признаков.

Обычно считают связь сильной, если r ³. 0,7; средней тесноты, при 0,5 £ r £ 0,7; слабой при г < 0,5. Не следует, особенно работая с ЭВМ, гнаться за большим числом знаков коэффициента корреляции. Во-первых, исходная информация редко имеет более трех значащих точных цифр, во-вторых, оценка тесноты связи не требует более двух значащих цифр.

Квадрат коэффициента корреляции называется коэффициентом детерминации:

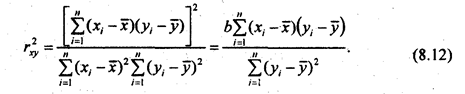
Эта формула понадобится при. анализе множественной корреляции. Умножив числитель и знаменатель (8.12) на 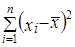получим:

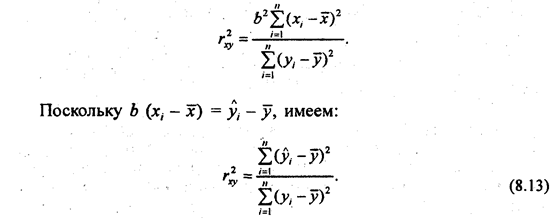
Это выражение соответствует выражению г\² (см. формулу (8.2)). Тождество коэффициента детерминации и квадрата корреляционного отношения служит основанием для интерпретации величины г² как доли общей дисперсии результативного признака у, которая объясняется вариацией признака-фактора х (и связью между вариацией обоих признаков). Собственно говоря, основным показателем тесноты связи и следовало бы считать коэффициент детерминации (для линейной формулы связи) или квадрат корреляционного отношения. Но исторически раньше был введен коэффициент корреляции, который долгое время и рассматривался как основной показатель.

Аналогично разным «рабочим» формулам для вычисления коэффициента регрессии можно на основе исходной формулы (8.10) подучить разные «рабочие» формулы коэффициента корреляции.

1. Разделив числитель и знаменатель формулы (8.11) на п, получим:

2.

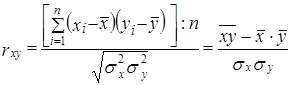. (8.14)

Эта формула соответствует формуле (8.8) для коэффициента регрессии.

2. Средние квадратические отклонения можно выразить через средние величины признака:

.

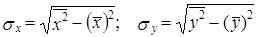Подставив эти выражения в (8.14), получим:

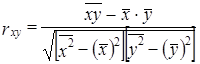. (8.15)

Эта формула (8.15) удобнее для расчетов, если средние величины признаков и средние квадраты индивидуальных величин вычислены ранее. Смысл же коэффициента корреляции раскрывается исходной формулой (8.11). В преобразованных формулах этот смысл не столь ясен.

Рассмотрим фактический пример анализа корреляционной парной линии связи по данным 16 сельхозпредприятий о затратах на 1 корову и о надое молока на корову. Ограниченный объем совокупности принят только в учебных целях, чтобы избежать приведения громоздких таблиц (табл. 8.1).

Средние значения признаков: x̅ = 1605 руб.; у̅ = 35,2 ц/голов.

Сопоставляя знаки отклонений признаков jc и у от средних величин, видим явное преобладание совпадающих по знакам пар отклонений: их 14 и только 2 пары несовпадающих знаков.

Таблица 8.1