В среднем от коровы

Номера единиц сово-куп-ности	Затраты на 1 корову, руб./голов х_i	Надой от 1 коровы, ц, y_i	x_i - x̅	y_i - y̅	(x_i - x̅) ´ ´ (y_i - y̅)	(x_i - x̅)²	(y_i - y̅)²	Расчетные значения надоя, ц i
		34,2	-3	-1,0	+3,0		1,00	35,1
		19,6	-406	-15,6	+6333,6		243,36	21,1
		27,3	-283	-7,9	+2235,7		62,41	25,3
		32,5	+73	-2,7	-197,1		7,29	37,7
		33,2	-5	-2,0	+10,0		4,00	35,0
		31,8	-250	-3,4	+850,0		11,56	26,5
		30,7	-192	^,5	+864,0		20,25	28,5
		32,6	-115	-2,6	+299,0		6,76	31,2
		26,7	+11	-8,5	-93,5		72,25	35,6
		42,4	+88	+7,2	+633,6		51,84	38,2
		37,9	+60	+2,7	+162,0		7,29	37,3
		36,6	+61	+1,4	+85,4		1,96	37,3
		38,0	+23	+2,8	+64,4		7,84	36,0
		32,7	-1	-2,5	+2,5		6,25	35,2
		51,7	+472	+16,5	+7788		272,25	51,6
		55,3	+466	+20,1	+9366,6		404,01	51,4
S 25678	563,2	-	-	+28473,7		1180,32	563,0

Немецкий психиатр Г. Т. Фехнер (1801 - 1887) предложил меру тесноты связи в виде отношения разности числа пар совпадающих и несовпадающих пар знаков к сумме этих чисел:

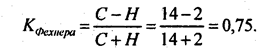
Конечно, коэффициент Фехнера - очень грубый показатель тесноты связи, не учитывающий величину отклонений признаков от средних значений, но он может служить некоторым ориентиром в оценке интенсивности связи. В данном случае он указывает на тесную связь признаков.

Вычислим на основе итоговой строки табл. 8.1 параметр парной линейной корреляции:

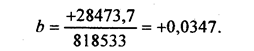
Он означает, что в среднем по изучаемой совокупности отклонение затрат на 1 корову от средней величины на 1 руб. приводило к отклонению с тем же знаком среднего надоя молока на 0,0347 ц, т. е. на 3,47 кг на корову. При нестрогой интерпретации говорят: «С увеличением затрат на корову на 1 руб. в среднем надой молока возрастал на 3,47 кг». Поскольку и до начала резкой инфляции стоимость 3,47 кг молока значительно превосходила рубль, увеличение затрат на корову было экономически целесообразным.

Свободный член уравнения регрессии вычислим по формуле (8.6):

а = 35,2 - 0,0347 • 1605 = - 20,49.

Уравнение регрессии в целом имеет вид:

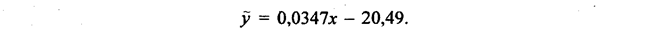
Отрицательная величина свободного члена уравнения означает, что область существования признака у не включает нулевого значения признакам и близких значений. Можно рассчитать минимально возможную величину фактора х, при которой обеспечивается наименьшее значение признака у (разумеется, положительное).

- это наименьшая сумма затрат на 1 корову, при которых корова способна давать молоко. Если же область существования результативного признака^включает нулевое значение признака-фактора, то свободный член является положительным и означает среднее значение результативного признака при отсутствии данного фактора, например среднюю урожайность картофеля при отсутствии органических удобрений.

Графическое изображение корреляционной связи по данным табл. 8.1. приведено на рис. 8.1.

Коэффициент корреляции, рассчитанный на основе табл. 8.1,

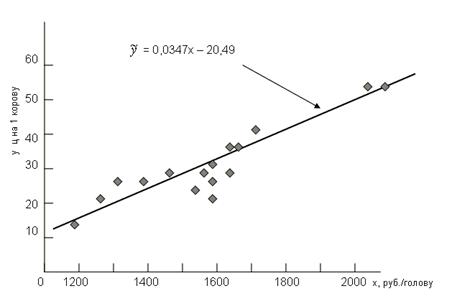
Рис. 8.1. Корреляция затрат на корову с продуктивностью

<90 91 929394 95 96 >

Дата добавления: 2015-01-21; просмотров: 942;