Расчет корреляции по аналитической группировке
| Группа предприятий по оборачваемости в днях | Число предприятий fj | Среднее число дней x'j | Средняя прибыль, млн руб. y̅j | y̅j - y̅ | (y̅j - y̅)2 | x' - x̅ | (x'j - x̅) ´ (y̅j - y̅) fj | (x'j - x̅)2fj | ỹxj | ( ỹxj - y̅)2 fj |
| А | ||||||||||
| 40-50 | 14,57 | 2,80 | 47,04 | -18 | -302,4 | 15,06 | 64,94 | |||
| 51 -70 | 12,95 | 1,18 | 11,14 | -3 | -28,0 | 12,36 | 2,78 | |||
| 71 - 101 | 7,40 | -4,37 | 114,58 | +23 | -603,0 | 7,69 | 99,88 | |||
| Итого | 11,77 | - | 172,76 | - | -933,4 | 11,77 | 167,60 |
Коэффициент линейной регрессии
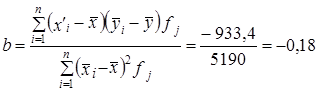 ,
,
свободный член уравнения регрессии
а = у̅ - bх̅ = 11,77 - (-0,18·63) = 23,15.
Итак, имеем уравнение связи: у̃ = 23,15 - 0,18х. Вычислим по этому уравнению расчетные значения прибыли у̃i для каждой группы. Подставив в уравнение середины интервалов групп х̅', запишем у̃i в графу 9 табл. 8.2. Вариация расчетных значений прибыли связана с влиянием оборачиваемости х. Найдем сумму квадратов отклонений прибыли за счет вариации оборачиваемости - факторную вариацию (графа 10 табл. 8.2). Для расчета общей вариации результативного признака была вычислена сумма квадратов отклонений по индивидуальным данным:
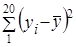 .
.
Эта сумма квадратов - общая вариация объема прибыли - равна 222,4. Теперь можем построить меры тесноты связи:
теоретическое корреляционное отношение
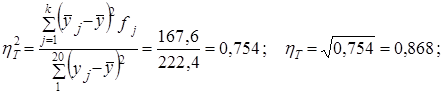
эмпирическое корреляционное отношение (рассчитанное в гл. б)
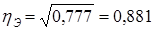 .
.
Оба квадрата корреляционных отношений соответствуют по содержанию ранее рассмотренному коэффициенту детерминации (8.1) и (8.2) и интерпретируются как Показатели доли вариации результативного признака, объясняемой за счет вариации группировочного, факторного признака (и, конечно, связанных с ним прочих факторов). В данном примере связь является тесной. Различие в том, что в эмпирическом корреляционном отношении связь признаков не абстрагирована от случайных влияний прочих факторов на вариацию у, не связанных с вариацией х.
Наиболее рациональным приемом анализа и расчета параметров корреляционной связи с помощью группировки является построение так называемой «корреляционной решетки» (табл. 8.3). Это таблица, в которой изучаемая совокупность сгруппирована одновременно по обоим признакам, связь между которыми изучается (двумерное распределение). Число групп по признакам может быть как равным, так и неравным. Если наибольшие числа частот каждой строки и каждого столбца располагаются на первой диагонали (в табл. 8.3 эти цифры подчеркнуты), связь является прямой и близкой к линейной; если наибольшие числа частот располагаются вдоль второй диагонали (в табл. 8.3 эти цифры также подчеркнуты), связь обратная, линейная. Если частоты во всех клетках таблицы примерно равны, связи нет; если наибольшие числа расположены по дуге, связь криволинейная. В табл. 8.3 кроме частот приведены строки и графы для расчета необходимых сумм при вычислении параметров корреляционной  связи.
связи.
В табл. 8.3 наибольшие частоты в строках и графах расположены вдоль первой диагонали, что говорит в соответствии с логикой о прямой линейной связи возрастов женихов и невест. Связь эта далеко не полная; как видим, «любви все возрасты покорны», все клетки таблицы заполнены, значит, существуют браки между лицами любых возрастов.
Как средние величины признаков, так и все суммы, входящие в расчет параметров корреляции, при группировке взвешиваются на соответствующие частоты, поэтому формулы (8.9) и (8.11) приобретают следующий вид:
 , (8.22)
, (8.22)
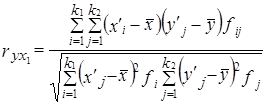 , (8.23)
, (8.23)
где x'i, yj. - середины интервалов i-й категории х и j-й категории y;
fi - частота i-го значения х;
fj - частота j-го значения у;
fij - частота совместного появления i-го значения х и j-гo значения у (это числа в клетках «корреляционной решетки»).
Взвешенные суммы квадратов отклонений подсчитаны и приведены в последней графе и в последней строке табл. 8.3. Для вычисления числителя в (8.22) и (8.23) необходимо умножить отклонения по обоим признакам (с учетом их знаков) на частоты совместного распределения и сложить все 25 произведений:
(-9).(-9,2)·18212 +1·(-9,2)·1914 + ... + 33·31,8·1701 = 5196031,6.
Это число записано в правом нижнем углу табл. 8.3. Рассчитаем параметры уравнения регрессии. Согласно (8.22)
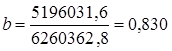
Это означает, что в среднем с увеличением возраста женихов на 1 год возраст их невест возрастал на 0,83 года. Свободный член уравнения согласно (8.6)
a = 29,0 - 0,83·31,2 = 3,1.
Уравнение имеет вид:
у̂ = 3,1 + 0,83·х.
Так как оба признака равноправны, то можно получить уравнение зависимости среднего возраста жениха от возраста невесты. Поменяв местами х и у, получаем:
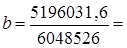 =0,859; а = 31,2 - 0,859·29 = 6,3; х̂ = 6,3 + 0,859у.
=0,859; а = 31,2 - 0,859·29 = 6,3; х̂ = 6,3 + 0,859у.
Коэффициент корреляции согласно формуле (8.23) составляет:

Коэффициент детерминации r2 = 71,3%, т. е. вариация возраста супруга или супруги на 71% зависит от вариации возраста «второй половины». Связь весьма тесная.
Конечно, расчет параметров корреляции на основе группировки является приближенным: реальные значения признаков заменяются серединами интервалов, а при открытых интервалах - их экспертными оценками. Не учитывается неравномерность изменения частот внутри интервалов. Казалось бы, с появлением программ для ЭВМ этот метод должен отмереть. Однако для больших совокупностей в десятки и сотни тысяч единиц большинство программ ввиду ограничений на объем оперативной памяти непригодно. Да и сам процесс занесения в память ЭВМ сотни тысяч чисел занял бы столь громадное время, что, выигрыш во времени расчета на ЭВМ был бы многократно превышен. Таким образом, иногда трудоемкость расчета с помощью группировки и простого калькулятора оказывается намного меньше, чем на ЭВМ, а степень точности достаточна для большинства задач анализа связи.
Дата добавления: 2015-01-21; просмотров: 1033;
