Параболическая корреляция
Линейные связи являются основными. Однако встречаются и нелинейные связи, хорошо описываемые параболой, гиперболой и т. д.
Уравнение регрессии в форме параболы 2-го порядка имеет следующий вид:

Если при линейной связи среднее изменение результативного признака на единицу фактора постоянно по всей области вариации фактора, то при параболической корреляции изменение признака х на единицу признака^ меняется равномерно с изменением величины фактора. В результате связь может даже поменять знак на противоположный, из прямой превратится в обратную, из обратной в прямую. Такой характер связи объективно присущ многим системам. Например, с увеличением дозы удобрений урожайность сель-хозкультур сначала повышается, но если превысить оптимальную величину дозы, то при дальнейшем росте дозы удобрений растения угнетаются и урожайность снижается.
Нормальные уравнения метода наименьших квадратов для параболы 2-го порядка таковы:
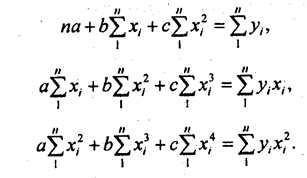
Если расчет производится не по индивидуальным данным, а на основе аналитической группировки, то уравнения МНК приобретают следующий вид:
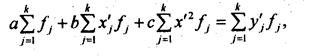
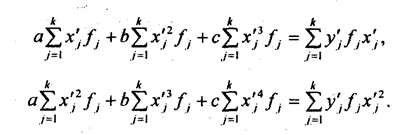
Решая эту систему, получаем значения параметров а, b и с. Показателем тесноты параболической корреляции является корреляционное отношение, вычисляемое как корень квадратный из выражения (8.2).
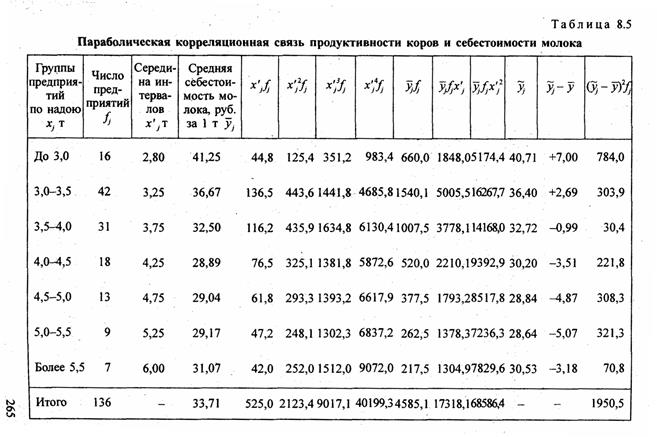
В качестве примера параболической корреляционной связи рассмотрим зависимость себестоимости молока от продуктивности коров по данным аналитической группировки сельхозпредприятий области (табл. 8.5). В этой же таблице приведены расчетные величины, входящие в уравнения МНК для параболы.
Были получены нормальные уравнения МНК:
136а + 5256 + 2123,4с = 4585,1, 525а+2123.4А + 9017,1с = 17318,1, 2123,4а + 9017,16 + 40199,3с = 68586,4.

Эта парабола имеет точку минимума в фактической области вариации факторного признака. Для нахождения значения фактора, при котором достигается минимальное значение результативного признака, следует приравнять нулю первую производную по х уравнения (8.30):
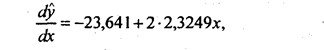
откуда х = 23,641/4,6498 = 5,084 т молока на корову.
Итак, минимальная себестоимость молока в совокупности предприятий, в условиях периода, к моторому относятся данные, достигалась в среднем при надое молока на корову 5084 кг. Значение фактора х при достижении минимума себестоимости можно назвать оптимальной продуктивностью коров, а сама задача его поиска - это одна из оптимизационных задач, решаемая математико-статистическим методом.
Для измерения тесноты параболической корреляционной связи находим вариацию результативного признака у, объясняемую вариацией фактора х как сумму квадратов отклонений расчетных величин у от средней величины у, взвешенных на число предприятий. Общая сумма квадратов отклонений всех 136 значений у, от средней величины составляет 4624,7. Таким образом согласно формуле (8.1), корреляционное отношение
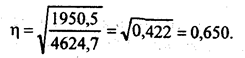

Дата добавления: 2015-01-21; просмотров: 1803;
