Глава II. СВОБОДНЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ НЕКОНСЕРВАТИВНОЙ СИСТЕМЕ

Консервативные системы являются идеализированными системами. Реальные системы неконсервативны, то есть их энергия меняется со временем. Рассмотрим системы, которые обладают потерями энергии. Уточним модели маятника и контура с учетом потерь.

Пусть маятник совершает колебания в вязкой среде. Тогда на него будет действовать сила вязкого трения, которая по определению;

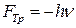, (2.1)

где 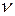– линейная скорость, 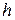– постоянный коэффициент.

Для простоты рассмотрения будем полагать, что сила трения приложена к центру тяжести маятника. Тогда 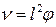и уравнение будет

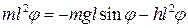, (2.2)

Вводя обозначение 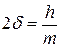, получим,

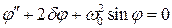, (2.3)

При малых углах отклонения

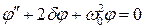. (2.4)

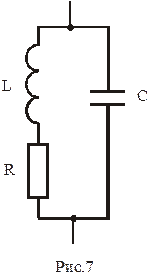Теперь получим уравнение контура с потерями. В электротехнических цепях потери моделируются активным сопротивлением. Опыт показывает, что существенными потерями являются потери в катушке. Следовательно, модель контура с потерями будет иметь вид, приведенный на рисунке 7.

Уравнение для заряда получим на основании второго правила Кирхгофа

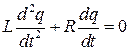(2.5)

Обозначим .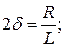

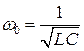Получим

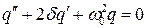(2.6)

Легко видеть, что движение маятника при малых углах отклонения с учетом вязкого трения и колебания заряда в контуре с потерями описываются одним и тем же линейным уравнением

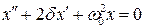. (2.7)

Коэффициент 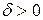называется коэффициент затухания, 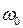- собственной частотой. При 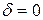получаем известное уравнение гармонического осциллятора.

С формальной точки зрения учет потерь, а в общем случае, неконсервативность, проявляется в том, что в уравнении движения появилось слагаемое, пропорциональное 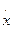. Более глубокое исследование показывает, что в неконсервативной системе «скорость» 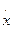может входить в нечетной степени .

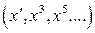Решим уравнение (2.7) и проанализируем, как движется во времени неконсервативная система. Уравнение линейное, с постоянными коэффициентами. Ищем решение методом Эйлера. Частное решение

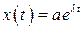, (2.8)

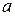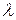где и - константы. Подставляя в дифференциал уравнение (2.7), сокращая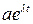 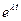, получим характеристическое уравнение:

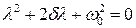. (2.9)

Корни этого уравнения:

,

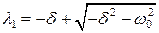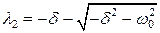. (2.10)

Общее решение:

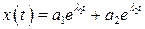. (2.11)

Где 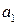и 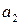определяются из начальных условий.

В зависимости от соотношени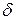й и 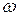различают два случая;

1) 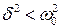- случай малого затухания, что соответствует колебательной системе;

2) 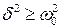- случай большого затухания (система апериодическая).

Рассмотрим подробнее первый случай.

Движение в колебательной системе ( )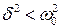

Обозначим

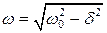. (2.12)

Тогда корни характеристического уравнения;

,

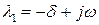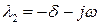, (2.13)

комплексные и сопряженные. Общее решение будет

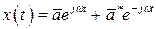. (2.14)

Представим комплексные постоянные в полярной форме:

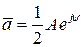, (2.15)

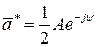, (2.16)

используя формулу Эйлера (1.11) перейдем к действительным величинам:

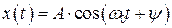, (2.17)

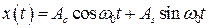. (2.18)

Соответствующие пары постоянных ( ), ( ), ( 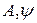) 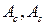определяются из начальных условий:

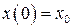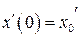, . (2.19)

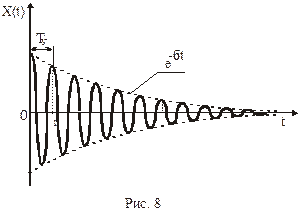На рис.8 приведен пример графика движения в системе с малыми потерями.

Движение является колебательным (знакопеременным), убывающим. При малом коэффициенте затухания близко к гармоническому колебанию, поэтому функцию часто называют «затухающей синусоидой». Колебание является непериодическим, так как ни при каких Т не выполнятся

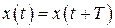. (2.20)

Однако вводят понятие условного периода 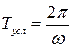, как интервал между одинаковыми переходами функции через 0.

Очевидно, что нули 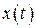совпадают с нулями 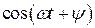. Частота 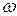является условной частотой. При малых затуханиях .

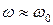Со временем колебания затухают вследствие потерь. Количественно затухание характеризуется любой из следующих констант:

1) 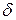- коэффициент затухания,

2) 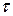- постоянная времени, или время релаксации,

3) 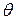- логарифмический декремент затухания,

4) 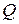- добротность системы.

Все эти константы взаимосвязаны и используются в конкретных случаях.

Коэффициент затухания 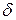входит в стандартную форму уравнения; имеет размерность, обратную времени.

Постоянная времени (время релаксации)

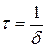. (2.21)

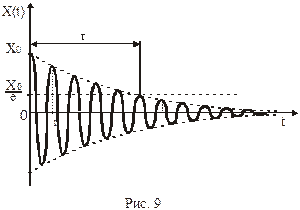Это интервал времени, в течении которого первоначальная амплитуда уменьшается в 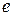раз 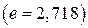(Рис.9).

Константы 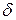и 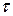являются размерными величинами, их значения зависят от выбора единицы измерения. Это не всегда удобно, поэтому вводят безразмерные величины: логарифмический декремент затухания 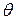и добротность .

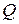По определению логарифмическим декрементом затухания называется величина

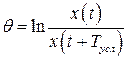, (2.16)

где 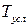- условный период. Подставляя 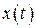, получим

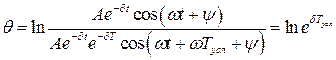, (2.17)

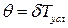. (2.18)

Чтобы пояснить физический смысл 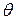, лучше взять обратную величину

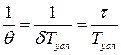. (2.19)

Видно, что 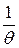есть число условных периодов, соответствующих уменьшению амплитуды в 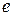раз.

Еще один безразмерный параметр, характеризующий потери – добротность. Получим его, предварительно преобразовав уравнение системы;

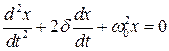. (2.20)

Введем так называемое собственное время системы

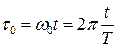. (2.21)

Смысл его очевиден: эталоном времени служит период собственных колебаний исследуемой системы. Текущее время измеряется в периодах. Множитель 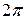означает, что время 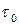оценивается в радианах.

Тогда производные связаны соотношениями

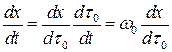, (2.22)

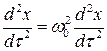. (2.23)

Подставляя их в уравнения и разделив все слагаемые на 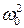, получим, что динамическое уравнение преобразуется к виду, который не зависит от диапазона частот:

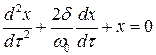. (2.24)

Единственная константа, которая обусловлена потерями в системе, это добротность

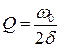. (2.25)

Системе без потерь соответствует .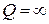

Добротность связана с логарифмическим декрементом затухания. Получим формулу связи:

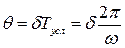. (2.26)

Условная частота:

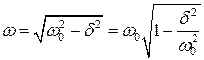(2.27)

или с учетом определения добротности;

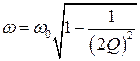. (2.28)

Точная формула, связывающая 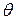и ;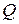

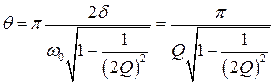, (2.29)

При больших добротностях с точностью до 1% справедливо простое соотношение

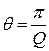. (2.30)

В этом же приближении условная частота равна собственной : .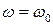

Применение 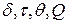зависит от конкретной задачи. Перечислим преимущественное использование конкретных параметров.

Коэффициент затухания 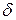используется в теоретических исследованиях, постоянную времени 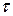- в теоретических и экспериментальных исследованиях, когда нужна временная оценка затухания амплитуды; логарифмический декремент затухания измеряется экспериментально и используется чаще всего при исследовании свободных колебаний; добротность используют при изучении вынужденных колебаний, так как её легко определить по резонансной кривой.

Анализ неконсервативной системы позволяет более строго решить вопрос о «жизненности» консервативной модели реальной системы.

Очевидно, что любой эксперимент длится конечное время наблюдения 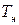. Если окажется, что время наблюдения много меньше «постоянной времени» системы 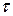, то экспериментатор не отметит изменения амплитуды колебаний и сделает вывод, что за время эксперимента энергия системы не изменилась, т.е. система консервативная. Таким образом, реальная система, в принципе неконсервативная, при конечном времени наблюдения, удовлетворяющим требованию 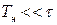, может рассматриваться как консервативная. А это в конечном счете упрощает теоретический анализ системы.