Идеальный контур как модель реального колебательного контура

Реальный контур состоит из катушки индуктивности и конденсатора. Реальная катушка не может считаться только индуктивностью, которая накапливает магнитную энергию. Во-первых, провод обладает конечной проводимостью, во-вторых, между витками накапливается электрическая энергия, т.е. имеет место межвитковая ёмкость. То же самое можно сказать и о емкости. Реальная емкость помимо самой емкости будет иметь в своем составе индуктивности выводов и сопротивление потерь.

Для упрощения задачи рассмотрим модель реального колебательного контура с катушкой индуктивности состоящей всего из двух витков.

Эквивалентная схема будет иметь вид, приведённый на рисунке на рис. 4. ( 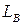и - и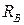ндуктивность и сопротивление одного витка, 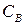- межвитковая ёмкость).

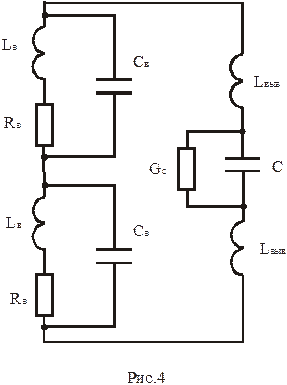Правая часть схемы описывает реальный конденсатор. Выводы конденсатора обладают паразитной индуктивностью 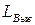, а среда между пластинами обладает потерями, что отражает проводимость 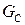. Нетрудно заметить, что такая электрическая схема является довольно сложной. Число контурных токов (т.е. независимых координат, или степеней свободы) равно 5. Следует также отметить, что реальные колебательные контура имеют катушки индуктивности с числом витков от десятков до нескольких сотен.

Однако, как показывает опыт радиоинженера, в большинстве случаев нет необходимости эту сложную схему.

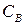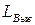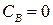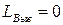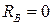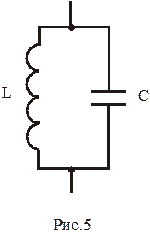
В умеренно высокочастотном диапазоне межвитковые ёмкости и паразитная индуктивность в силу своей малости практически роли не играют и ими можно пренебречь ( , ). Если не учитывать потери ( , 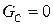), то получаем математическую модель, известную как «идеальный контур» (Рис.5). Его движение описывается одной переменной, в качестве которой возьмём заряд на ёмкости.

Уравнение для электрической цепи, изображенной на рис. 5 получим на основе закона Кирхгофа. Используем второе правило: сумма падений напряжений на элементах контура равна алгебраической сумме внешних ЭДС, включенных в этот контур. В нашем случае ЭДС равна нулю, и получим:

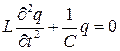(В.12)

Разделим слагаемые на 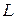и обозначим

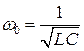(В.13)

Уравнение для идеального контура примет вид:

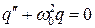(В.14)

Имея модели двух динамических систем, можно уже сделать некоторые выводы.

Простое сравнение уравнений (В.6) и (В.9) показывает, что маятник при малых отклонениях и идеальный контур описываются одним и тем же уравнением, известным как уравнение гармонического осциллятора, которое в стандартной форме имеет вид:

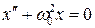(В.15)

Следовательно, и маятник, и контур как колебательные системы обладают одинаковыми свойствами. Это и есть проявление единства колебательных систем.

Имея эти модели, уравнения, их описывающие, и обобщая полученные результаты, дадим классификацию динамических систем по виду дифференциального уравнения. Системы бывают линейные и нелинейные.

Линейные системы описываются линейными уравнениями (см. (В.11) и (В.15)). Нелинейные системы описываются нелинейными уравнениями (например, уравнение математического маятника (В.9)).

Другим признаком классификации является число степеней свободы. Формальным признаком служит порядок дифференциального уравнения, описывающего движение в системе. Система с одной степенью свободы описывается уравнением 2-го порядка (или двумя уравнениями первого порядка); система с N степенями свободы описывается уравнением или системой уравнений порядка 2N.

В зависимости от того как изменяется энергия колебательного движения в системе , все системы делятся на два класса: консервативные системы – те, у которых энергия остаётся неизменной, и неконсервативные системы – те, у которых энергия изменяется с течением времени. В системе с потерями энергия убывает, однако возможны случаи, когда энергия возрастает. Такие системы называются активными.

Динамическая система может подвергаться и не подвергаться внешнему воздействию. В зависимости от этого различают четыре типа движения.

1.Собственные, или свободные колебания, системы. В этом случае от внешнего источника система получает конечный запас энергии и источник отключается. Движение системы при конечном начальном запасе энергии и представляет собственные колебания.

2.Вынужденные колебания. Система находится под действием внешнего периодического источника. Источник оказывает «силовое» воздействие, т.е. природа источника та же, что и у динамической системы (в механической системе – источник силы, в электрической – ЭДС и т.д.). Колебания обусловленные внешним источником, называются вынужденными. При отключении они исчезают.

3.Параметрические колебания наблюдаются в системах, у которых периодически во времени изменяется какой-либо параметр, например, ёмкость в контуре или длина маятника. Природа внешнего источника который, изменяет параметр, может отличаться от природы самой системы. Например, ёмкость можно изменять механически.

Нужно отметить, что строгое разделение вынужденных и параметрических колебаний возможно лишь для линейных систем.

4.Особый вид движения – автоколебания. Термин впервые введён академиком Андроновым. Автоколебание – это периодическое колебание, период, форма и амплитуда которого зависят от внутреннего состояния системы и не зависят от начальных условий. С энергетической точки зрения автоколебательные системы являются преобразователями энергии некоторого источника в энергию периодических колебаний.

Глава 1.СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ КОНСЕРВАТИВНОЙ СИСТЕМЕ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ (ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР)

Уравнение такой системы имеет вид:

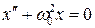(1.1)

(примерами могут служить математический маятник при малых углах отклонения и идеальный колебательный контур). Решим уравнение (1.1) подробно, пользуясь классическим методом Эйлера. Ищем частное решение в виде:

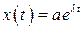, (1.2)

где 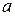и 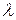– постоянные, пока неизвестные константы. Подставим (1.2) в уравнение (1.1)

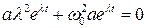. (1.3)

Разделим обе части уравнения на 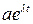и получим алгебраическое, так называемое характеристическое, уравнение:

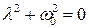. (1.4)

Корни этого уравнения

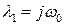, (1.5)

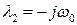, (1.6)

где 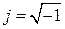– мнимая единица. Корни мнимые и комплексно-сопряжённые.

Как известно, общее решение есть сумма частных, т.е.

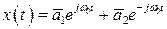. (1.7)

Мы полагаем, что 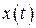есть действительная величина. Чтобы это выполнялось, постоянные 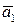и 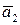должны быть комплексно сопряженными, т.е.

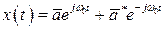. (1.8)

Две постоянные 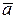и 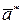определяются из двух начальных условий:

,

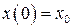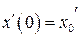
Решение в форме (1.8) преимущественно используется в теории; для прикладных задач оно не удобно, так как 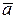и 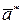не измеряются. Перейдём к форме решения, которое наиболее употребительно на практике. Представим комплексные постоянные в полярной форме:

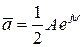, (1.9)

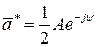. (1.10)

Подставим их в (1.8) и воспользуемся формулой Эйлера

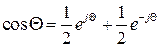, (1.11)

тогда

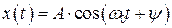, (1.12)

где 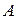- амплитуда колебаний, 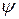- начальная фаза.

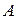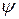и определяются из начальных условий. Заметим, что начальная фаза зависит от начала отсчёта во времени. Действительно, постоянную 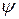можно представить в виде:

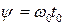, (1.13)

тогда

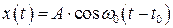. (1.14)

Если начало отсчёта во времени совпадает с 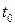, начальная фаза равна нулю. Для гармонического колебания сдвиг по фазе и сдвиг во времени эквивалентны.

Разложим косинус в (1.13) на косинусоидальную и синусоидальную составляющие. Получим ещё одно представление:

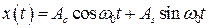, (1.15)

где

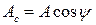, (1.16)

. (1.17)

Есл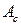и и 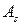известны, то нетрудно найти амплитуду и фазу колебания, используя следующие соотношения:

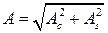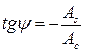, . (1.18)

Все три формы записи (1.8, 1.12, 1.15) эквивалентны. Использование конкретной формы определяется удобством рассмотрения конкретной задачи.

Анализируя решение, можно сказать, что собственные колебания гармонического осциллятора есть гармоническое колебание, частота которого зависит от параметров системы и не зависит от начальных условий; от начальных условий зависят амплитуда и начальная фаза.

Независимость от начальных условий частоты (периода) собственных колебаний называется изохорностью.

Рассмотрим энергию гармонического осциллятора на примере колебательного контура. Уравнение движения в контуре

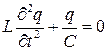. (1.19)

Умножим слагаемые этого уравнения на :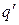

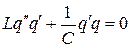. (1.20)

После преобразования его можно представить в виде:

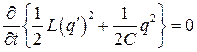. (1.21)

Так как 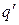есть ток 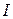, то

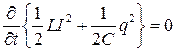, (1.22)

где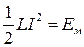-есть мгновенное значение магнитной энергии в индуктивности, а 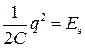–электрической энергии в ёмкости.

Полная энергия, запасенная контуром:

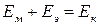. (1.23)

Из (1.7) получим 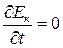, т.е. 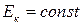- энергия контура остается постоянной, не зависит от времени. Мы приходим к выводу, что система консервативна.

Что же происходит с магнитной и электрической энергией в отдельности? Закон изменения заряда на конденсаторе нам известен – (1.12) и

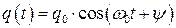, (1.24)

тогда

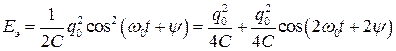. (1.25)

Найдем закон изменения энергии в конденсаторе. Ток в емкостной ветви можно найти используя следующее выражение

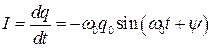. (1.26)

Подставив (1.28) в формулу для нахождения электрической энергии получим закон изменения электрической энергии на конденсаторе

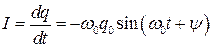, (1.27)

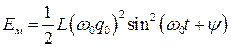. (1.28)

С учетом

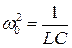(1.29)

. (1.30)

Таким образом, энергия в каждом элементе контура колеблется с удвоенной частотой. График этих колебаний приведен на рис. 6.

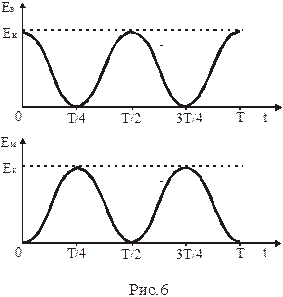В начальный момент времени вся энергия сосредоточена в емкости, магнитная энергия ровна нулю. По мере разряда емкости через индуктивность электрическая энергия из емкости переходит в магнитную энергию индуктивности. Через четверть периода вся энергия сосредотачивается в индуктивности, т.е. емкость полностью разрядилась. Затем этот процесс периодически повторяется.

Таким образом, колебание в идеальном контуре – это переход электрической энергии в магнитную и обратно, периодически повторяющийся во времени.

Этот вывод справедлив для любых электромагнитных колебательных систем, в частности для объемных резонаторов, где магнитная и электрическая энергия пространственно не разделены.

Обобщая этот результат, можно утверждать, что колебательный процесс в линейной консервативной системе – это периодический переход энергии одного типа в другой. Так, при колебаниях маятника кинетическая энергия переходит в потенциальную и наоборот.