Математический маятник как модель физического маятника
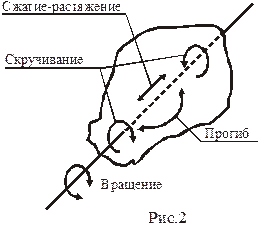
 Любое тело, способное вращаться вокруг своей оси, называется физическим маятником. Если тело не является абсолютно упругим, то, как известно из опыта, что кроме вращения, возможны другие типы движения, такие как сжатие и растяжение тела вдоль оси, скручивание и прогиб (Рис.2). Причем все перечисленные виды движения могут происходить независимо друг от друга. Следовательно, все четыре типа движения независимы и количественно описываются каждый своими параметрами или, как говорят в механике, координатами. Здесь мы подходим к определению понятия степень свободы. По определению число степеней свободы равно числу независимых координат, которые полностью описывают движение системы.
Любое тело, способное вращаться вокруг своей оси, называется физическим маятником. Если тело не является абсолютно упругим, то, как известно из опыта, что кроме вращения, возможны другие типы движения, такие как сжатие и растяжение тела вдоль оси, скручивание и прогиб (Рис.2). Причем все перечисленные виды движения могут происходить независимо друг от друга. Следовательно, все четыре типа движения независимы и количественно описываются каждый своими параметрами или, как говорят в механике, координатами. Здесь мы подходим к определению понятия степень свободы. По определению число степеней свободы равно числу независимых координат, которые полностью описывают движение системы.
При создании физической модели исследователю предстоит выбрать различное число степеней свободы. Очевидно что, чем больше степеней свободы, тем ближе модель к реальной системе, но тем сложнее её математическое описание и нахождение решения полученных математических уравнений.
Вернёмся к физическому маятнику. Если рассматриваемое тело выполнено из твердого материала, например, стали или чугуна, то из опыта можно сделать вывод, что основным видом движения является вращение, так как сжатие растяжение или скручивания для такого тела практически отсутствуют и ими можно пренебречь в силу их малости. Т.е. в данном случае, чтобы исключить другие виды движения, достаточно принять, что тело не сжимаемо или абсолютно упруго.
Следующий шаг в упрощении модели: вся масса тела m считается сосредоточенной в точке, расположенной в центре тяжести, и эта точка соединена с осью вращения невесомым и не сжимаемым стержнем длины 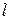 . И последняя довольно сильная идеализация – отсутствие потерь.
. И последняя довольно сильная идеализация – отсутствие потерь.
 Получили модель физического маятника – математический маятник. В качестве независимой координаты используем угол
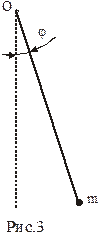
Получили модель физического маятника – математический маятник. В качестве независимой координаты используем угол 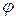 отклонения вертикальной оси проходящей через точку подвеса (Рис.3). Величины
отклонения вертикальной оси проходящей через точку подвеса (Рис.3). Величины 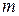 и
и 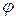 постоянны.
постоянны.
Для количественного описания физической модели системы воспользуемся законом Ньютона для вращательного движения
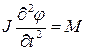 , (В.6)
, (В.6)
где Ј – момент инерции, который по определению равен 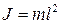 , а
, а 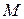 – момент сил, равный
– момент сил, равный 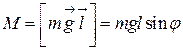 . Подставляя
. Подставляя 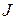 и
и 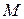 , получим:
, получим:
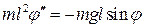 .
.
Поделив на 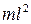 и преобразуя, имеем:
и преобразуя, имеем:
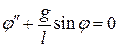 . (В.7)
. (В.7)
Обозначим
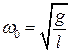 , (В.8)
, (В.8)
тогда уравнение для колебаний математического маятника принимает классический вид:
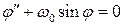 . (В.9)
. (В.9)
При малых углах отклонения справедливо
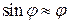 (В.10)
(В.10)
и уравнение для маятника упрощается
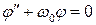 (В.11)
(В.11)
Рассмотрим ещё один пример конструирования модели.
Дата добавления: 2015-01-13; просмотров: 2725;
