Энергетические соотношения в системе с малым затуханием
Рассмотрим эти соотношения на пример колебательного контура с потерями. Уравнение его:
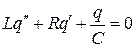 , (2.31)
, (2.31)
умножим на 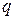 и преобразуем;
и преобразуем;
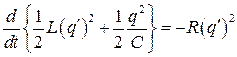 . (2.32)
. (2.32)
Полная энергия, запасенная в контуре:
 , (2.33)
, (2.33)
где
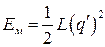 , (2.34)
, (2.34)
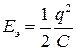 . (2.35)
. (2.35)
После преобразования получим следующее выражение:
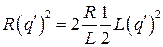 (2.36)
(2.36)
и с учетом ранее введенных обозначений:
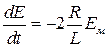 . (2.37)
. (2.37)
Изменение энергии за период
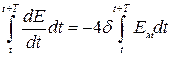 (2.38)
(2.38)
или
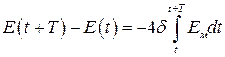 , (2.39)
, (2.39)
если 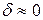 , то средняя за период энергия, запасенная на индуктивности
, то средняя за период энергия, запасенная на индуктивности
 . (2.40)
. (2.40)
Где 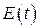 - энергия всего контура.
- энергия всего контура.
Отсюда:
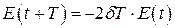 , (2.41)
, (2.41)
 . (2.40)
. (2.40)
Отсюда еще одно определение добротности
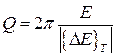 . (2.41)
. (2.41)
Т.е. это число, которое показывает, во сколько раз энергия, запасенная в колебательной системе, больше, по сравнению с потерями за период колебаний.
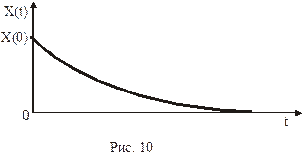 Завершим рассмотрение линейной неконсервативной системы краткой сводкой результатов для системы с большим затуханием (рис.10). Для этого случая
Завершим рассмотрение линейной неконсервативной системы краткой сводкой результатов для системы с большим затуханием (рис.10). Для этого случая 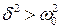 и при
и при 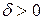 корни характеристического уравнения
корни характеристического уравнения 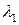 ,
, 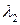 действительные и отрицательные:
действительные и отрицательные:
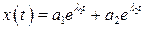 , (2.42)
, (2.42)
показывает, что при 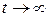 функция
функция 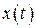 монотонно (экспоненциально) стремится к 0.
монотонно (экспоненциально) стремится к 0.
Движение будет лимитационным, т.е. ограниченным по амплитуде. Некоторые особенности движения возможны вблизи начала движения и зависят они от начальных условий. Соответствующие типы движений будут рассмотрены специально методом фазовой плоскости.
Критический случай 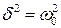 представляет только математический интерес, так как на практике никогда не реализуется. Общее решение имеет вид ;
представляет только математический интерес, так как на практике никогда не реализуется. Общее решение имеет вид ;
 . (2.43)
. (2.43)
Тип движения качественно тот же, что и при 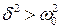 .
.
Дата добавления: 2015-01-13; просмотров: 994;
