ВВЕДЕНИЕ. Поскольку количество движения СМТ равно произведению массы CМТ на скорость центра масс СМТ (4.16), то уравнению (8.8) можно придать иную форму:

Поскольку количество движения СМТ равно произведению массы CМТ на скорость центра масс СМТ (4.16), то уравнению (8.8) можно придать иную форму:

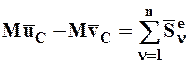, (8.10)

где М – масса СМТ, а 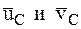– скорости центра масс СМТ в начале и в конце удара.

Уравнение (8.10) представляет выражение теоремы о движении центра масс СМТ при ударе:

Теорема: Изменение при ударе количества движения центра масс СМТ, в котором сосредоточена вся ее масса, равно геометрической сумме импульсов всех внешних ударных сил, действующих на СМТ.

Из уравнения (8.10) видно, что внутренние ударные импульсы, возникающие, например, при столкновении тел, входящих в состав данной СМТ, не изменяют скорости центра масс этой СМТ.

Проектируя обе части равенства (8.10) на координатные оси, получим:

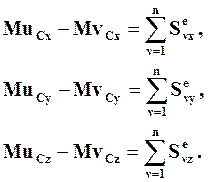(8.11)

Из соотношений (8.11) следует, что изменение за время удара проекции на какую-нибудь ось количества движения центра масс СМТ, в котором сосредоточена вся ее масса, равно сумме проекций на ту же ось импульсов внешних ударных сил, действующих на СМТ.

Параграф 6. Теорема об изменении кинетического момента СМТ при ударе

Рассмотрим основное уравнение теории удара для n-й МТ рассматриваемой СМТ:

.

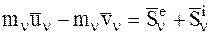Обозначим радиус-вектор n-й точки СМТ относительно начала О инерциальной системы координат через 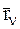. Как было показано в пункте 8.2, положение n-й точки за время удара не изменится, а следовательно, за это время не изменится и ее радиус-вектор .

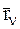Составив такие же уравнения для всех n МТ рассматриваемой СМТ, а затем умножив обе части равенства векторно слева на радиус-вектор 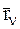и сложив их почленно, получим:

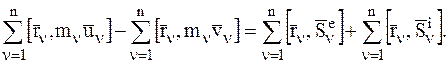
Введем следующие обозначения:

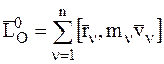– кинетический момент СМТ относительно центра О до удара,

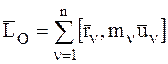– кинетический момент СМТ относительно центра О после удара.

Так как внутренние ударные импульсы равны по модулю и противоположны по направлению, то геометрическая сумма их моментов относительно любого центра равна нулю. Поэтому полученное уравнение с учетом обозначений примет вид:

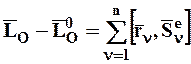
или (8.12)

.

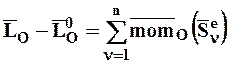Это уравнение представляет выражение теоремы об изменении кинетического момента СМТ при ударе.

Теорема: Изменение за время удара кинетического момента СМТ относительно какого-нибудь неподвижного центра равно геометрической сумме моментов импульсов внешних ударных сил, действующих на СМТ, относительно того же центра.

Проектируя соотношение (8.12) на координатные оси, получим скалярную форму теоремы об изменении кинетического момента при ударе:

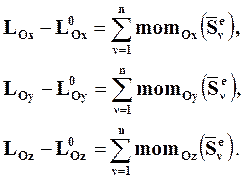(8.13)

Из соотношений (8.13) следует, что изменение за время удара кинетического момента СМТ относительно какой-либо неподвижной оси равно сумме моментов импульсов внешних ударных сил, действующих на СМТ, относительно той же оси.

Используя соотношения (8.12) и (8.13), можно получить два следствия, аналогичных двум следствиям, полученным для этой теоремы в главе 4.

ВВЕДЕНИЕ

Теория колебаний, как самостоятельная дисциплина, оформилась в 30-х гг. нашего столетия. В 1931 году советский ученый акаде­мик Л.Н. Мандельштам впервые прочитал курс лекций по теории колеб­аний.

Первые исследования колебательных процессов связаны с именами Г.Галилея и Х. Гюйгенса и относились к изучению колебаний маятника. XVIII- XIX вв. изучались в основном механические колебания. Наибольший вклад внес английский физик Рэлей. Его труд “Теория звука”, написанный в 80-х годах прошлого столетия, завершил теорию малых колебаний. Первые работы по теории нелинейных колебаний, связанной с небесной механикой, принадлежат французскому математику А. Пуан­каре. Большое влияние на развитие теории колебаний оказали работы по устойчивости движения русского математика А.М. Ляпунова. Бурное развитие радиотехники в начале нашего столетия стимулировало развитие нелинейной теории колебаний. Первые ощутимые результаты были получены голландским ученым Ван-дер-Полем.

При этом каждый из вышеназванных исследователей использовал свои математические подходы к описанию колебательных процессов.

Поэтому в 30-х гг. прошлого столетия возникла идея объединения результатов исследования различных по своей природе колебательных процессов в рамках единой теории.

Строгое обоснование его результатов, а главное создание общей теории колебаний, принадлежит академику Мандельштаму. Значительный вклад в развитие теории колебаний внесли советские ученые, ученики Мандельштама: академик А.А. Андронов, К.Ф. Теодорчик, В.В. Мигулин и другие.

Отличительной особенностью теории колебаний является то, что отсутствует разделение колебательных систем на электрические и механические. Поэтому специалисты, владеющие вышеуказанной теорией легко осваивают новые специальности, что в условиях рыночной экономики является важным фактором.

В настоящее время теория колебаний является классической дис­циплиной и читается во многих ВУЗах. Ее методы оказываются весьма плодотворными в различных разделах науки и техники.

Цель курса – исследование колебательных процессов в различных динамических системах.

Методы анализа, применяемые в теории колебаний, будут даваться без доказательств, а их изложение носит справочный характер. Поскольку курс читается студентам радиотехнических специальностей, пред­почтение отдается изучению радиоэлектронных динамических систем. Однако понимание сущности явлений позволит быстро разобраться в физике процесса любой другой системы, как электрической, так и механической.

Итак, что же является предметом изучения в теории колебаний?

В повседневной жизни мы постоянно сталкиваемся с движением физических объектов. Даже то, что не способно изменять свое местоположение в пространстве, тем не менее, находится в постоянном движении. Примером таких систем могут служить различные по своему происхождению предметы. Деревья, мачты освещения, телевизионные антенны совершают движения вблизи своего состояния равновесия под действием внешних факторов. И это только то – что доступно человеческому взору. Аналогичные процессы происходят внутри сложных механических и электрических систем, которыми мы тоже пользуемся в своей повседневной жизни.

Поэтому, прежде чем приступать к изложению конкретных вопросов, необходимо дать определение термина «колебание».

Наиболее распространенным в настоящее время и общепринятым является следующее определение.

Колебание – это ограниченное, повторяющееся движение системы около некоторого состояния (состояния равновесия).

Ранее было сказано, что в теории колебаний нет разделения колебательных систем на механические и электрические.

Колебательные процессы, в теории колебаний,классифицируется по кинематическим признакам: форме и периоду колебаний. Будем считать, что колебательный процесс описывается функцией времени 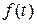. Процесс будет периодическим, если он описывается периодической функцией. По определению периодическая функция удовлетворяет условию (1) при любом Т.

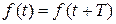(В.1)

Наименьшая постоянная Т называется периодом. Если колебание не удовлетворяет условию (В.1), то колебание является не периодическим. Таким образом, все колебательные процессы делятся на два больших класса периодические и непериодические.

Среди периодических колебаний особое место занимают гармонические колебания. Это связано с тем, что гармонические колебания являются наиболее естественными колебаниями, которые встречаются в природе. По этой причине получить и использовать данный вид колебаний достаточно просто. К тому же с точки зрения математики описание гармонических колебаний и дальнейшее их исследование не вызывает никаких трудностей.

Если колебание может быть описано в виде

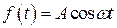(В.2)

или

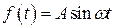, (В.3)

где ω- круговая частота.

Кроме того, существует класс почти периодических колебаний. Функции, описывающие эти колебания, удовлетворяют условию

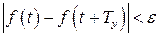, (В.4)

где 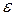– заданная положительная малая величина, 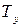– «почти период».

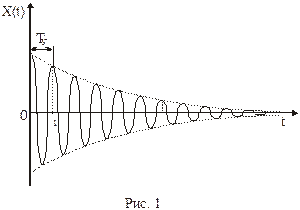
Примером таких колебаний могут служить затухающие колебания, для которых условие (1) не выполняется из-за того, что с каждым новым периодом амплитуда колебаний будет уменьшаться. Однако, как видно из рис.1, близка к периодической.

Колебания такого вида могут быть описаны следующей формулой:

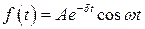, (В.5)

где 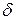– коэффициент затухания.

В настоящее время интенсивно изучаются случайные колебания, но модели и методы исследования в этой области отличны, от классической теории колебаний и поэтому рассматриваться не будут.

Классификация по кинематическим признакам не является единственной, так как не может отразить все или большинство свойств колебаний. Более разнообразной и содержательной является классификация по признакам, присущим динамическим системам.

Но необходимо подчеркнуть, что классификация относится к моделям, а не к реальным системам. Поэтому прежде чем рассматривать отдельные признаки динамических систем, ниже будут рассмотрены примеры построения моделей двух различных по своей физической природе колебательных систем: физического маятника (механическая система) и колебательного контура (электрическая система).

Теория колебаний как и любая другая теория включает в себя следующие четыре этапа.

Первый и особенно важный - это выбор модели реальной системы. Построение модели достаточно простой, но отражающей суть, является творчеством, требует глубокого понимания предмета исследования, и предложить здесь какой, либо рецепт невозможно. Ниже на примерах маятника, контура будет показано, как создается физическая модель реальной системы.

Второй этап - математическое описание модели. На этом этапе основные физические признаки описанные на первом этапе переводятся на язык математических формул. В результате чего получается математическая модель динамической системы, представляющее из себя уравнение или систему уравнений.

Третий этап – математический. Ищется решение уравнения - точное или приближенное. Приводится анализ решения.

Четвертый этап - сравнение результатов теории с экспериментом. Если совпадение удовлетворительное, говорят о том, что теория явления построена. Если результаты расчета не согласуются с экспериментом, значит модель не адекватна явлению и требует уточнения или замены.

Рассмотрим на простых примерах принципы создания математических моделей реальных систем.