Схема однофакторного дисперсионного анализа

Источник вариации	Сумма квадратов отклонений D	Число степеней свободы d.f.	Средний квадрат отклонений s2=D:d.f.	F-критерий
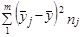
Между группами		m-1	s21
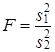
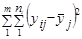
Внутри групп		n-m	s22
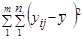
Общая		n-1	s2

По данным табл. 6.6 проверим гипотезу Н₀ : m ₁= m₂ ..., т. е. предположим, что оборачиваемость средств никак не влияет на прибыль.

D_факт = 172,76, d.f._факт =3-1=2, s²₁ = 86,38;

D_ост – D_общ - D_факт = 224,4 - 172.76 = 51,64;

d.f._ост = 20 - 3=17; s²₂ = 3,03.

Тогда F = 28,5. Критическое значение F-критерия из табл. 3 приложения F_{(a=0,05, d.f.1=2, d.f.2=17)} = 3,59. Таким образом F_факт > F_крит следовательно, Н₀ отклоняется. Действительно, скорость оборота средств является очень важным фактором формирования прибыли, на это указывало и значение эмпирического корреляционного отношения h = 0,881.

Рассмотрим двухфакторный дисперсионный анализ, основой проведения которого служит комбинационная группировка по двум факторам х и z, с последующим разложением дисперсии результативного признака у:

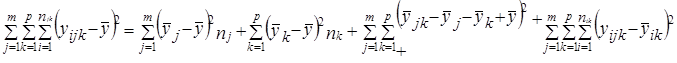(7.44)

где i - номер единицы в j-й группе по признаку х и k-й по признаку z;

j = 1̅,т̅,

k =I̅р̅, у̅_jk - среднее значение признака у̅ в группе, образованной ком-бинацией j-го значения признака х и k-го значения признака z;

у̅_j - среднее значение признака у в j-й группе по признаку х;

y̅_k - среднее значение признака у в k-й группе по признаку z;

у̅ - общая средняя признака y в целом по выборке;

п_jk - число единиц в группе, образованной комбинацией j-го значения признака х и k-го значения признака z;

п_j - число единиц в j-й группе по признаку х,

п_k - число единиц в k-й группе по признаку z;

т Р т р

п- общее число единиц,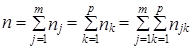

Равенство (7.44) можно записать так:

D_общ = D_x + D_z + D_xz + D_ост (7.45)

где D_ч - вариация у под влиянием фактора x;

D_z - вариация у под влиянием фактора z;

D_xz - вариация у, обусловленная взаимодействием факторов х и z;

D_ост - вариация у под влиянием прочих факторов.

Первые три слагаемые составляют вариацию признака у, вызванную изучаемыми факторами, поэтому равенство (7.45) можно записать в виде:

D_общ = D_факт +D_ост (7.46)

где

D_факт = D_х + D_z + D_xz. (7.47)

Величина D_факт может быть рассчитана не через составляющие, а непосредственно как

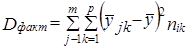(7.48)

Однако при неравенстве численностей подгрупп п_jk и групп п_j и п_k равенство нарушается (за счет взвешивания при неравных весах).

Поэтому рассчитываются невзвешенные величины:

;

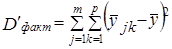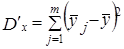; (7.49)

;

.

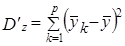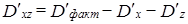Затем на основе сравнения взвешенной (7.48) и невзвешенной величин факторной дисперсии находят поправочный коэффициент:

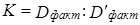(7.50)

Этот коэффициент используется для корректировки невзвешенных сумм квадратов отклонений 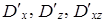, на основе которых проводят расчет F-критериев:

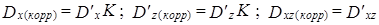(7.50)

Число степеней свободы для каждой суммы квадратов отклонений составляет:

d.f._x=m- 1; d.f._z = p - 1; d.f._xz = (m-1)(p -1) = mp - т - р + 1,

в целом

d.f._факт = d.f._x + d.f._z + d.f._xz = mp-1;

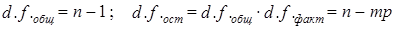(7.51)

В двухфакторном дисперсионном анализе испытуемые гипотезы формулируются следующим образом:

1. Н₀ : m_1∙ = m_2. =…m_m

2. Н₀ : m_1∙ = m_2. =…m_p

3. Н₀ : m_1∙ = m_2. =…m_mp

Вся процедура двухфакторного дисперсионного анализа обобщается в табл. 7.10.

Таблица 7.10