Схема двухфакторного дисперсионного анализа

Источник вариации	Сумма квадратов отклонений D	Число степеней. свободы d. f.	Средний квадрат отклонений s2 = D/d.f.	F-критерий
Факторы х и z	D¢факт∙K	mp - 1	s2факт
Фактор х	D¢x∙K	m - 1	s2x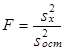
Фактор z	D¢z∙K	p - 1	s2z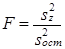
Взаимодействие факторов х и z	(D¢факт- D¢x- - D¢z)∙K	mp – p-m+1	s2xz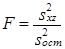
Остаточная	Dобщ - D¢факт∙K	n - mp	s2ост
Общая	Dобщ	n - 1	s2

Решение о первой гипотезе принимается на основе сравнения

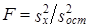с .

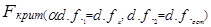Если F_факт > F_крит,то Н₀ отклоняется.

Вторая гипотеза испытывается на основе сравнения

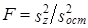c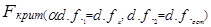

Третья - на основе сравнения

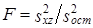c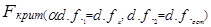

Во всех случаях, если F_факт > F_крит, Н₀ отклоняется. На основе F-критерия принимаются решения о форме уравнения регрессии, о статистической значимости той или иной объясняющей переменной при построении многофакторного уравнения регрессии (см. гл. 8) и др.

Рассмотренные направления проверки статистических гипотез охватывают лишь важнейшие из них. Процедура испытания статистических гипотез применяется для определения того, случайно или нет полученное значение коэффициента корреляции, коэффициента вариации и т. д., случайны или нет различия в значениях показателей (медиан, коэффициентов корреляции, регрессии и т.д.) в разных совокупностях. Во всех случаях результатом является вероятностное суждение, которое составляет сущность анализа данных в разнообразных сферах: в медицине, биологии, технике, политике, спорте, экономике, психологии и социологии.