Проверка гипотезы о средних величинах

Основные гипотезы о средних величинах следующие: гипотезы о значении генеральной средней (при известной генеральной дисперсии или при неизвестной генеральной дисперсии); гипотезы о равенстве генеральных средних нормально распределенных сово-купностей (при известных генеральных дисперсиях, при неизвестных равных генеральных дисперсиях, при неизвестных неравных генеральных дисперсиях).

Первая задача чаще всего решается при неизвестной генеральной дисперсии. Испытуемая гипотеза Н₀ : m = m₀, альтернативная гипотеза Н₁: m ≠ m₀. Испытание гипотезы проводят с помощью t- критерия. При большом числе наблюдений критическое значение критерия определяется по таблице интеграла вероятностей, при малом - по таблице распределения Стьюдента с заданным уровнем значимости и числом степеней свободы, п — 1.

Если испытуемая гипотеза Н₀: m = а, то фактическое значение критерия представляет отношение оцениваемой разности к средней возможной ошибке выборочной средней.

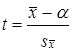, (7.36)

где 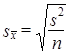- при большой выборке;

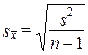- при малой выборке.

Если t_факт > t_крит , Н₀ не отклоняется, если t_факт < t_крит , H₀ отклоняется.

Рассмотрим пример.Часовая выработка забойщика при добыче угля в шахте по норме составляет 400 кг. Фактическая выработка соответствовала норме. При переходе в новый забой условия работы забойщиков усложнились. Для проверки обоснованности нормы в новых условиях был проведен учет работы 9 забойщиков: их средняя часовая выработка составила 388 кг с дисперсией, равной s² = 171.

Выдвигается гипотеза о том, что норму выработки пересматривать не нужно, т.е. Н₀ : m = 400 кг. Проверим эту гипотезу на 5%-нюм уровне значимости. Критическое значение t-критерия определяется по таблице распределения Стьюдента при доверительной вероятности 0,95 (1 - 0,05) и числе степеней свободы d.f. =- n - 1 = 8. Критическое значение составит t_крит = 2,3. Фактические значения t-критерия вычисляются по формуле (7.36):

.

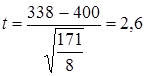Поскольку t_факт > t_крит Н₀ отклоняется. Норма выработки в новых условиях должна быть пересмотрена, так как производительность труда стала существенно ниже нормативной.

В рассмотренном примере различие между фактическим и таб-~ личным значениями /-критерия невелико, поэтому вывод недостаточно надежен. Надежность вывода вообще понижается, если нет уверенности в нормальном распределении генеральной совокупности.

Гипотеза о равенстве средних может рассматриваться как гипотеза о связи, если сопоставляются средние величины, обусловленные действием какого-либо фактора. Например, сравнивается средняя заработная плата рабочих двух специальностей. Нулевая гипотеза состоит в том, что специальность рабочего не влияет на заработок. Если окажется, что t_факт > t_крит, нулевую гипотезу отклоняют и делают вывод о том, что специальность оказывает влияние на заработную плату.

Рассмотрим решение этой задачи при условии, что генеральные дисперсии неизвестны, но принимаются равными. При сравнении средних величин выдвигается гипотеза, что обе выборки принадлежат одной и той же генеральной совокупности со средней m и дисперсией s².

При неизвестной генеральной дисперсии формула t-критерия имеет вид:

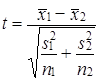. (7.37)

Поскольку s²₁ и s²₂ рассматриваются как выборочные оценки общей дисперсии s², то формула (7.37) может быть записана так:

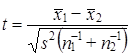, (7.38)

где x̅₁, x̅₂ - выборочные средние; s² - выборочная оценка общей дисперсии;

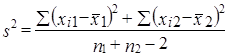.(7.39)

Гипотеза H₀ отклоняется, если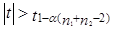

Рассмотрим пример. Для проверки устойчивости цен на яблоки в летний период на двух рынках города проведено выборочное обследование: на первом рынке по данным 15 продавцов определена средняя цена, равная 2 тыс. руб./кг. при среднем квадратическом отклонении s² = 0,5 тыс. руб.; на втором рынке обследовано 17 продавцов, средняя цена оказалась равной 2,5 тыс. руб./кг, s² = 0,4 тыс. руб.

Н₀ : m = m₀, Н₁: m ≠ m₀.

.

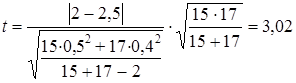При a = 0,05 и d.f. = 30, t_крит = 2,042, t_факт > t_крит , H₀ отклоняется, т. е. различия в ценах на двух рынках нельзя объяснить лишь случайностями выборки.

Проверка той же нулевой гипотезы при односторонней критической области будет проводиться на следующих условиях определения: t_крит : 1 - 2a и d.f. = n₁ + n₂ -2. Следовательно, если Н₁ : m₁ = m₂ (2a = 0,1, d.f. = 30), так что H₀ опять-таки отклоняется.

Случай проверки гипотезы о средних величинах при неизвестных дисперсиях, равенство которых не предполагается, здесь не рассматривается ввиду его недостаточной теоретической разработанности[6].