Теоретические частоты
| Формы собственности | Оценка возможностей деятельности | |||||
| крайне неблагоприятно | неблагоприятно | трудно сказать | благоприятно | исключительно благоприятно | итого | |
| Один владелец | 11,6 | 12,7 | 8,3 | 17,1 | 7,3 | |
| Товарищество | 8,2 | 8,9 | 5,9 | 11,9 | 5,1 | |
| Товарищество с ограниченной ответственностью | 12,2 | 13,4 | 8,8 | 18,0 | 7,6 | |
| Итого |
Таким было бы распределение ответов о возможностях деятельности, если бы формы собственности никак не сказывались. Задавая уровень значимости a = 0,05, наводим по табл. 4 приложения критическое значение критерия c22 a, df при числе степеней свободы d.f. = (3 - 1)(5-1) = 8. Отсюда c22 a, df = 15,51.
Различия между фактическими и теоретическими клеточными частностями обобщаются в величине c2:
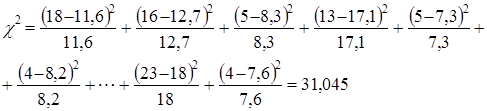
Так как c2факт > c2крит, Н0 отклоняется, т.е. форма собственности небезразлична для деятельности кафе и ресторанов. Таким образом, наблюдаемое значение c2 является значимым на 5%-ном уровне значимости, и нулевая гипотеза может быть отвергнута в пользу альтернативной.
Итак, мы рассмотрели один из возможных способов ответа на вопрос: существует ли связь между двумя переменными? Для этого мы выдвинули нулевую гипотезу, что такой связи нет, а затем рассмотрели способ статистического испытания этой гипотезы. Мы можем оценить величину риска в принятии предположения о существовании связи. Но означает ли это, что данная связь существенна с точки зрения ее силы? Вовсе не обязательно. Вопрос о силе или степени, тесноте зависимости — это иной вопрос, отличный от вопроса о существовании взаимосвязи.
В социально-экономических исследованиях, как правило, установление факта наличия связи между переменными не самоцель. Установив наличие связи, исследователь должен измерить ее силу (тесноту) с тем, чтобы иметь возможность сравнивать взаимосвязи между различными характеристиками, выделять наиболее сильные из них (см. гл. 8).
Дата добавления: 2015-01-21; просмотров: 848;
