Возможной вариации
| Номера единиц совокупности | Значения признака xi | Отклонения от средней xi -x̅ | Модули отклонений |xi - x̅| | Квадраты отклонений (хi - х̅)2 |
| ∙ ∙ ∙ n | х̅п ∙ ∙ ∙ | х̅(п - 1) -x̅ -x̅ • • -x̅ | х̅(п - 1) х̅ х̅ ∙ ∙ ∙ х̅ | х̅2(п - 1)2 х̅2 х̅2 ∙ ∙ ∙ х̅2 |
| Итого | х̅п | 0 (нуль) | 2х̅(п - 1) | х̅2[(п - 1)2+(n-1)] |
Исходя из выражений, стоящих в итоговой строке табл. 5.8, получаем следующие максимально возможные значения показателей вариации.
Средний модуль отклонений, или среднее линейное отклонение:
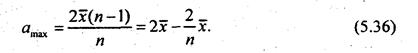
Среднее квадратическое отклонение:
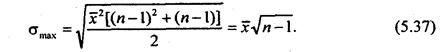
Относительное модульное (линейное) отклонение:

Коэффициент вариации:

Что касается квартального расстояния, то система с максимально возможной вариацией обладает вырожденной структурой распределения признака, в которой не существуют («не работают») характеристики структуры: медиана, квартили и им подобные.
Исходя из полученных формул максимально возможных значений основных показателей вариации, прежде всего следует вывод о зависимости этих значений от объема совокупности п. Эта зависимость обобщена в табл. 5.9.
Наиболее узкие пределы изменения и слабую зависимость от численности совокупности обнаруживают средний модуль и относительное линейное отклонение. Напротив, среднее квадратическое отклонение и коэффициент вариации сильно зависят от численности единиц совокупности. Эту зависимость следует учитывать при сравнении силы интенсивности вариации в совокупностях разной численности. Если в совокупности шести предприятий коэффициент вариации объема продукции составил 0,58, а в совокупности из 20 предприятий он составил 0,72, то справедливо ли делать вывод о большей неравномерности объема продукции во второй совокупности? Ведь в первой, меньшей, он составил 0,58 : 2,24 = 25,9% максимально возможного, т.е. предельного, уровня концентрации производства в одном предприятии из шести, а во второй, большей совокупности, наблюдаемый коэффициент вариации составил только 0,72 : 4,36 = 16,5% максимально возможного.
Таблица 5.9
Дата добавления: 2015-01-21; просмотров: 1038;
