Характеристика эксцесса распределения
С помощью момента четвертого порядка характеризуется еще более сложное свойство рядов распределения, чем асимметрия, называемое эксцессом.

Рис. 5.3. Асимметрия, распределения
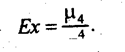
|
Показатель эксцесса рассчитывается по формуле
(5.30)
Часто эксцесс интерпретируется как «крутизна» распределения, но это неточно и неполно. График распределения может выглядеть сколь угодно крутым в зависимости от силы вариации признака: чем слабее вариация, тем круче кривая распределения при данном масштабе. Не говоря уже о том, что, изменяя масштабы по оси абсцисс и по оси ординат, любое распределение можно искусствен но сделать «крутым» и «пологим». Чтобы показать, в чем состоит эксцесс распределения, и правильно его интерпретировать, нужно сравнить ряды с одинаковой силой вариации (одной и той же величиной σ) и разными показателями эксцесса. Чтобы не смешать эксцесс с асимметрией, все сравниваемые ряды должны быть симметричными. Такое сравнение изображено на рис. 5.4.
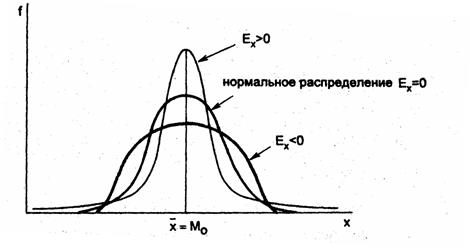
Рис.5.4. Эксцесс распределений
Для вариационного ряда с нормальным распределением значе- i ний признака показатель эксцесса, рассчитанный по формуле (5.30), j равен трем.
Однако такой показатель не следует называть термином «эксцесс», что в переводе означает «излишество». Термин «эксцесс» следует применять не к самому отношению по формуле (5.30), а к сравнению такого отношения для изучаемого распределения с величиной данного отношения нормального распределения, т.е. с величиной 3. Отсюда окончательные формулы показателя эксцесса, т.е. излишества в сравнении с нормальным распределением при той же силе вариации, имеют вид:
для ранжированного ряда
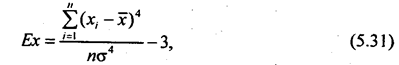
для интервального и дискретного вариационного ряда
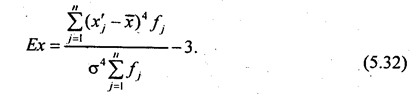
Наличие положительного эксцесса, как и ранее отмеченного значительного различия между малым квартальным расстоянием и большим средним квадратическим отклонением, означает, что в изучаемой массе явлений существует слабо варьирующее по данному признаку «ядро», окруженное рассеянным «гало». При существенном отрицательном эксцессе такого «ядра» нет совсем.
По значениям показателей асимметрии и эксцесса распределения можно судить о близости распределения к нормальному, что бывает существенно важно для оценки результатов корреляционного и регрессионного анализа, возможностей вероятностной оценки прогнозов (см. главы 7,8,9). Распределение можно считать нормальным, а точнее говоря - не отвергать гипотезу о сходстве фактического распределения с нормальным, если показатели асимметрии и эксцесса не превышают своих двукратных средних квадратических отклонений Стц, и <т^. Эти средние квадратические отклонения вычисляются по формулам:
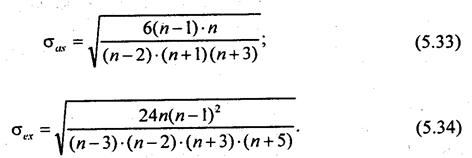
Дата добавления: 2015-01-21; просмотров: 1631;
