Предельные значения показателей вариации объемного признака при разных численностях совокупности
| Численность совокупностей | Максимальные значения показателей | |||||
| R | ρ | α | m | σ | v | |
| 2х | х̅ | х̅ | ||||
| 4х | 1,5 х̅ | 1,5 | 1,73 х̅ | 1,73 | ||
| б | 6х | 1,67 х̅ | 1,67 | 2,24 х̅ | 2,24 | |
| 10х | 1,80 х̅ | 1,80 | 3 х̅ | 3.00 | ||
| 20x | 1,90 х̅ | 1,90 | 4,36 х̅ | 4,36 | ||
| 50х | 1,96 х̅ | 1,96 | 7 х̅ | 7,00 | ||
| 100х | 1,98 х̅ | 1,98 | 9,95 х̅ | 9,95 | ||
| ∞ | ∞ | ∞ | 2 х̅ | ∞ | ∞ |
Имеет практическое значение и такой показатель, как отношение фактического среднего модуляотклонений к предельно возможному. Так, для совокупности шести предприятий это соотношение составило: 0,47 : 1,67 = 0,281, или 28,1%. Интерпретация полученного показателя такова: для перехода от наблюдаемого распределения объема продукции между предприятиями, к равномерному распределению потребовалось бы перераспределить
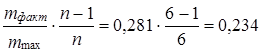, или 23,4% общего объема продукции в совокупности. Если степень фактической концентрации производства (фактическая величина σ или v) составляет некоторую долю предельного значения при монополизации производства на одном предприятии, то отношение фактического показателя к предельному может характеризовать степень концентрации (или монополизации) производства.
Отношения фактических значений показателей вариации или изменения структуры к предельно возможным используются также при анализе структурных сдвигов (см. главу 11).
Рекомендуемая литература к главе 5
1. Джини К. Средние величины. - М.: Статистика, 1970.
2. Кривенкова Л. Н., Юзбашев М. М. Область существования показателей вариации и ее применение // Вестник статистики. - 1991. - №6. - С. 66-70.
3. Пасхавер И. С. Средние величины в статистике. - М.: Статистика. 1979.
4. Шураков В. В., Дайитбегов Д. М. и др. Автоматизированное рабочее место статистической обработки данных (Глава 4. Предварительная статистическая обработка данных). - М.: Финансы и статистика, 1990.
Дата добавления: 2015-01-21; просмотров: 803;