Установление функции распределения показателей надежности по данным статистической информации.

Наиболее полной характеристикой надежности сложной системы является закон распределения, выраженный в виде функции распределения, плотности распределения или функции надежности. О виде теоретической функции распределения можно судить по эмпирической функции распределения (рис. 6), которая определяется из соотношения:

Fi =тi/N (42)

где mi - число отказов на интервале t; N — объем испытаний; ti ≤ t ≤ ti+1 - интервал времени, на котором определяют эмпирическую функцию.

Построение эмпирической функции осуществляют, суммируя приращения, полученные на каждом интервале:

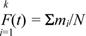(43)

где k - число интервалов.

Эмпирическая функция надежности является функцией, противоположной функции распределения; ее определяют по формуле:

Рi(t) = 1 – тi/N (44)

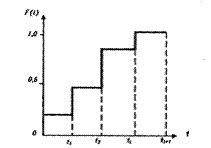
Рис. 6. Эмпирическая функция распределения.

Оценку плотности вероятности находят по гистограмме. Построение гистограммы сводится к следующему. Всю область значений времени t разбивают на интервалы t1, t2,…, ti и для каждого из этих интервалов определяют оценку плотности вероятности по формуле:

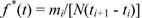(45)

где mi - число отказов на i-м интервале; (ti+1 - ti) - отрезок времени i -го интервала; N — объем испытаний; i = 1,2,..., k - число интервалов.

Графически гистограмма может иметь вид, изображенный на рис. 7.

Рис. 7.

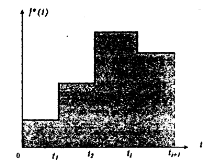
Рис. 7. Гистограмма.

Сглаживая ступенчатую гистограмму плавной кривой, можно по ее виду судить о законе распределения случайной величины. В практике для сглаживания кривой чаще всего используют метод наименьших квадратов. Для более точного установления закона распределения необходимо, чтобы число интервалов было не менее пяти, а число реализаций, попадающих в каждый интервал, - не менее десяти.

Графическое определение вида функции состоит в нанесении полученных экспериментальных данных на вероятностную бумагу, представляющую собой лист бумаги, на котором в прямоугольной системе координат нанесена сетка, при этом по оси ординат - шкала, соответствующая функции закона распределения (например, нормального, логарифмически-нормального и т.д.), а по оси абсцисс - линейная или логарифмическая шкала. Основная идея графического метода построения - подбор такой непрерывной замены координат, при которой график функции распределения становится прямой линией. Если такую замену переменных удалось отыскать, то на плоскости координат любая функция распределения этого семейства будет прямой линией (рис.8.)

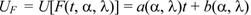(46)

где F(t, α, λ) - функция распределения, содержащая два неизвестных параметра.

Вероятностная бумага может быть использована не только для определения вида распределения, но и для нахождения параметров закона распределения. Оценки параметров закона распределения находят по углу наклона прямой и отрезкам, которые она отсекает на осях координат, для чего решают систему уравнений:

k = a(α, λ), (47)

c = b(α, λ),

где k = tg(ϕ) - тангенс угла наклона прямой линии к оси абсцисс; с - длина отрезка от точки пересечения прямой с осью абсцисс до оси ординат.

Если опытные точки располагаются на вероятностной бумаге близко к прямой, то это свидетельствует о соответствии опытных данных тому закону распределения, для которого построена вероятностная бумага.

Для нормального закона распределения справедливо следующее уравнение прямой:

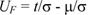(48)

где μ и σ - параметры распределения.

При построении вероятностной бумаги для этого распределения на горизонтальной оси откладывают равномерную шкалу для t, а на вертикальной оси - значения UF и надписывают величину F(t), поэтому шкала на вертикальной оси получается неравномерной. Область изменения t определяется разностью:

Δt = tmax – tmin. (49)

Если за ширину графика принять величину L [мм], то откладываемые на горизонталь ной оси значения t рассчитывают с помощью соотношения:

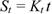(50)

где

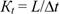(51)

Для построения шкалы функции распределения F(t) задаются ее минимальным [Fmin(t)] и максимальным [Fmax(t)] значениями, например Fmin(t) = 0,001, Fmax(t) = 0,999. Тогда для UF наименьшее значение будет U(Fmin) = -3,09, а наибольшее U(Fmax) = 3,09. Поэтому уравнение для SF при длине шкалы L = 300 мм записывают в следующем виде:

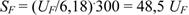(52)

Из уравнения (48) следует, что при F(t) = 0,5, UF = 0, а при F(t) <0,5 используют соотношение:

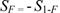(53)

На рис. 8 дан график функции распределения на вероятностной бумаге. Прямая пересекает ось t в точке μ (это следует из уравнения (48)).

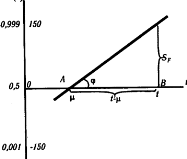
Рис. 8. График функции нормального распределения на вероятностной бумаге.

Для определения параметра σ воспользуемся уравнениями (48), (50) и (52). Из этих уравнений следует:

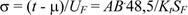(54)

где АВ - длина отрезка, равная t - μ , мм.

Из уравнения (54) и в соответствии с рис. 8 получим

σ = (48,5/Kt)ctg ϕ. (55)

Значение Kt известно, а ctg ϕ находят по графику.

При построении вероятностной бумаги для экспоненциального закона преобразуем уравнение функции распределения

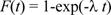(56)

к линейному виду:

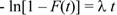(57)

Вероятностную бумагу для экспоненциального распределения (рис. 9) строят следующим образом: на горизонтальной оси откладывают равномерную шкалу для t, на вертикальной оси - значения, определяемые по формуле (57), и надписывается F(t). Наименьшее значение Fmin(t) = 0, наибольшее примем равным Fmax(t) = 0,999. Тогда для – ln[1 – F(t)] получаем наибольшее значение 6,908. Поэтому уравнение для SF запишем в таком виде:

SF = -300 ln[1 - F(t)]/6,908 = - 43,4 ln[1 - F(t)]. (58)

Параметр λ находим по уравнению:

λ = -ln[1 - F(t)]/t = SFKt/(43,4 St) = (Kt/43,4)tg ϕ. (59)

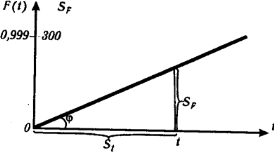
Рис. 9. Функция экспоненциального распределения на вероятностной бумаге.

При построении вероятностной бумаги для закона распределения Вейбулла (рис.10) функция 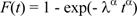(60)

преобразуется к линейному виду:

y = ln{ln[1- F(t)]} = α ln(λ t) = 2,303 α[lg t - lg(1/λ)]. (61)

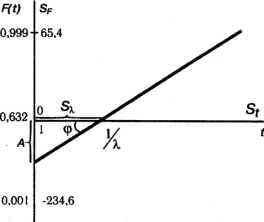
Рис. 10. График функции распределения Вейбулла на вероятностной бумаге.

На горизонтальной оси откладывают логарифмическую шкалу в соответствии с уравнением:

St = Kt lg t, (62)

где Kt - масштабный фактор.

На вертикальной оси откладывают значения y, а надписывают величину F(t). Примем для F(t) крайние значения: 0,001 и 0,999. Для этих значений ymin = -6,91 и уmax =1,93, т.е. размах величины у равен 8,84. Поэтому уравнение для SF имеет вид

SF = 300 y/8,84 = 33,94 y. (63)

Следует подчеркнуть, что при F(t) < 0,6321 имеем SF < 0 и при F(t) > 0,6321 имеем SF> 0.

Из уравнения (63) следует, что у = 0 при t = 1/λ. Поэтому значение 1/λ находят в точке пересечения графика с осью t.

Параметр α находят при решении уравнения

α = Kt tg ϕ/78,16. (64)

При построении вероятностной бумаги для других законов распределения используют изложенный выше метод.