Распределение Вейбулла.

Закон Вейбулла представляет собой деухпараметрическое распределение. Этот закон является универсальным, так как при соответствующих значениях параметров превращается в нормальное, экспоненциальное и другие виды распределений. Автор данного закона использовал его при описании экспериментально наблюдавшихся разбросов усталостной прочности стали, пределов ее упругости. Закон Вейбулла удовлетворительно описывает наработку до отказа подшипников, элементов радиоэлектронной аппаратуры, его используют для оценки надежности деталей и узлов машин, в частности автомобилей, а также для оценки надежности машин в процессе их приработки. Плотность распределения описывается зависимостью

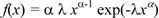(29)

где α — параметр формы кривой распределения; λ — параметр масштаба; е =2,71828 — основание натурального логарифма.

График плотности распределения дан на рис. 4.

Функция распределения Вейбулла

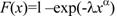(30)

Функция надежности для этого закона:

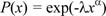(31)

Математическое ожидание случайной величины X равно:

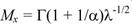(32)

где Г(х) — гамма-функция. Для непрерывных значений х

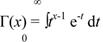(33)

Для целочисленных значений х гамма-функцию вычисляют по формуле

Г(x) = (x -1)!; (34)

(35)

(36)

Дисперсия случайной величины равна:

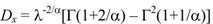(37)

Рис. 4. Плотность распределения Вейбулла для λ=1

Широкое применение закона распределения Вейбулла объясняется тем, что этот закон, обобщая экспоненциальное распределение, содержит дополнительный параметр α. Подбирая нужным образом параметры α и λ, можно получить лучшее соответствие расчетных значений опытным данным по сравнению с экспоненциальным законом, который является однопараметрическим (параметр λ).

Так, для изделий, у которых имеются скрытые дефекты, но которые длительное время не стареют, опасность отказа имеет наибольшее значение в начальный период, а потом быстро падает. Функция надежности для такого изделия хорошо описывается законом Вейбулла с параметром α<1.

Наоборот, если изделие хорошо контролируется при изготовлении и почти не имеет скрытых дефектов, но подвергается быстрому старению, то функция надежности описывается законом Вейбулла с параметром α>1. При α =3.3 распределение Вейбулла близко к нормальному.