Интерференция в тонких пленках.

При освещении тонкой плоскопараллельной плёнки или пластинки с показателем преломления n происходит наложение двух световых волн, возникающих в результате деления падающей волны. Первая из них образуется в результате отражения от передней поверхности пленки в точке А (луч 1 на рис 2). Вторая волна образуется в результате преломления исходной волны,

отражения от задней поверхностей плёнки в точке В и последующего преломления в точке С (луч 2). Для плоскопараллельной пластинки постоянной толщины, равной d, интерференционная картина наблюдается в фокальной плоскости линзы, собирающей лучи 1 и 2.

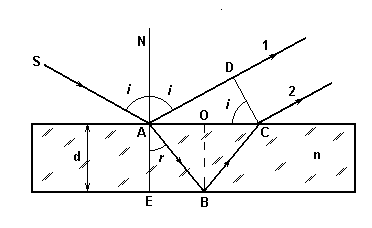
Рис.2. Интерференция света в тонкой пленке.

До точки А оптическая разность хода между этими лучами отсутствует. Оптическая длины пути луча 1 от точки А до точки D составит L₁ = n_в AD + λ/2 (n_в - показатель преломления воздуха; будем считать, что n_в = 1). Дополнительное слагаемое λ/2 возникает из-за того, что, отражение волны в точке А происходит от оптически более плотной среды (т.е. от среды с более высоким показателем преломления). В этом случае фаза отраженной волны скачкообразно изменяется на π. Это можно представить как рост оптической длины пути луча 1 на величину, равную половине длины волны в вакууме. Так как при отражении волны от оптически менее плотной среды (отражение в точке В от воздуха) изменения фазы не происходит, то оптическая длина пути луча 2 равна L₂ = n(AB + ВС). Линза не вносит дополнительной разности хода для параллельных лучей, исходящих из точек, лежащих в одной плоскости, перпендикулярной этим лучам. Линза лишь преобразует плоскую волну в сходящуюся сферическую волну. Поэтому разность хода между лучами 1 и 2, исходящими из точек C и D, не изменится в точке наложения лучей Р.

Оптическая разность хода, возникающая между лучами 1 и 2 от источника S до точки наложения лучей Р будет равна

Δ_опт = L ₂ - L₁ = n (АВ + ВС) - (AD + λ /2).

Отсюда имеем:

Δ_опт = 2nАВ - AD – λ /2 (6)

Из треугольников ABО и ADC следует, что

AD = AC sin i, AC = 2АО = 2d tg r, AD = 2d sin i tg r; АВ = d / cos r

Подставив два последние выражения в (6), получим:

Δ_опт = 2nd/cos r – 2d tg r sin i – λ /2 (7)

По закону преломления света на границе двух сред sin i = n sin r, тогда

sin r = sin i / n; cos r = 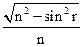, tg r = .

Подставив два последних выражения в (7), после простых преобразований получим:

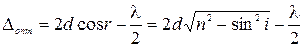
Пусть плоскопараллельная пластинка (d = const) освещается монохроматическим рассеянным светом (что обеспечивает различные углы падения i). Для некоторого угла падения величина Δ_опт для лучей 1 и 2 будет одинаковой независимо от положения точки А на поверхности пластины,. При наложении пар лучей от всей поверхности пластинки с помощью линзы будут наблюдаться интерференционные полосы, каждая из которых соответствует одному и тому же углу падения. Поэтому их называют полосами равного наклона. Они имеют вид чередующихся концентрических светлых и темных колец. Если толщина пластинки не постоянна (например, клинообразная пластинка), то при освещении ее параллельным пучком лучей (т.е. при одном и том же угле падения i = const) для лучей, отраженных от обеих поверхностей, условия максимума или минимума выполняются для определенных участков с одинаковой толщиной. Светлые или темные полосы, образованные при отражении света участками пластины с одинаковой толщиной, поэтому называют интерференционными полосамиравной толщины. Для клиновидной пластинки они имеют вид прямоугольных светлых и темных полос, параллельных ребру.