Интерференция волн

Согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов связывают с понятием когерентности. Волны называются когерентными, если разность их фаз остается постоянной во времени. Очевидно, что когерентными могут быть лишь волны, имеющие одинаковую частоту. При наложении в пространстве двух (или нескольких) когерентных волн в разных его точках получается усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих волн. Это явление называется интерференцией волн.

Рассмотрим наложение двух когерентных сферических волн, возбуждаемых точечными источниками S₁ и S₂(рис. 221), колеблющимися с одинаковыми амплитудой A₀и частотой wи постоянной разностью фаз.

Рис. 221

Согласно (154.7),

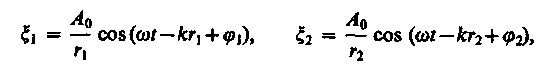
где r_lи г₂ — расстояния от источников волн до рассматриваемой точки В, k — волновое число, j₁и j²— начальные фазы обеих накладывающихся сферических волн. Амплитуда результирующей волны в точке В по (144.2) равна

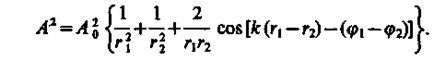
Так как для когерентных источников разность начальных фаз (j₁ - j₂) = const, то результат наложения двух волн в различных точках зависит от величины D = г₁ – r₂, называемой резвостью хода волн.

В точках, где

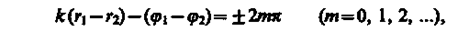(156.1)

наблюдается интерференционный максимум: амплитуда результирующего колебания A = |A₀/r₁ + A₀r₂| . В точках, где

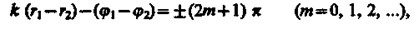(156.2)

наблюдается интерференционный минимум: амплитуда результирующего колебания A = |A₀/r₁ - A₀r₂|; m = 0, I, 2, ..., называется соответственно порядком интерференционного максимума или минимума.

Условия (156.1) и (156.2) сводятся к тому, что

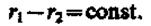(156.3)

Выражение (156.3) представляет собой уравнение гиперболы с фокусами в точках S₁ и S₂.Следовательно, геометрическое место точек, в которых наблюдается усиление или ослабление результирующего колебания, представляет собой семейство гипербол (рис. 221), отвечающих условию j₁ - j₂ = 0. Между двумя интерференционными максимумами (на рис. 221 сплошные линии) находятся интерференционные минимумы (на рис. 221 штриховые линии).