Интерференция полей антенны и ее зеркального изображения

Складывая выражения (5.11) и (5.13), получим

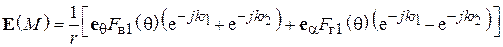. (5.14)

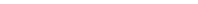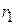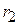В выражении (5.14) следует учесть, что расстояния и в дальней зоне из-за параллельности лучей О1М и О2М (рис. 5.5) могут быть представлены в виде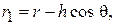 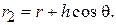Далее вместо угла места сферической системы координат 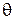бу­дет использоваться угол возвышения 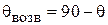(рис. 5.6). Тогда получим

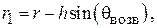
. (5.15)

В этом случае

,

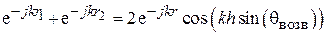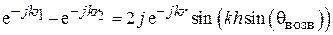. (5.16)

С учетом (5.14) и (5.16) окончательное выражение для поля в точке М примет вид

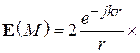
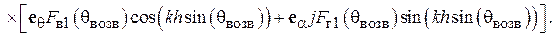(5.17)

Векторная функция в квадратных скобках (5.17) называется характеристикой направленности антенны, поднятой над идеально проводящей поверхностью. Заметим сразу, что проводящая плоскость может существенно изменить поляризационные свойства поля антенны. Пусть, например, 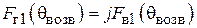, т. е. поле антенны 1 имеет круговую поляризацию. Тогда выражение для суммарного поля излучения поля в точке наблюдения М (см. рис. 5.5) примет вид:

.

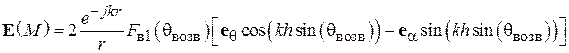Как видно, 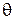-я и 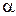-я компоненты поля 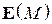находятся либо в фазе (при одинаковых знаках обеих компонент), либо в противофазе (при противоположных знаках). В обоих случаях это линейная поляризация. При этом с изменением угла 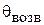соотношение 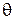-й и 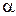-й компонент изменяется, так что изменяется и ориентация линейно поляризованного вектора электрического поля.