Вопрос 4: Интерференция от двух источников.

Пусть две когерентные волны исходят из источников S₁ и S₂, колебания в них направлены перпендикулярно к плоскости чертежа, и наблюдение производится в точке М. Если, обе волны имеют одинаковые амплитуды, то колебания в М, вызываемые первой и второй волнами, выразятся в виде

s₁ = a cos 2π(t/T- d₁/λ),

s₂ = a cos [2π(t/T- d₂/λ) - φ],

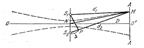где d₁= S₁M и d₂ = S₂M, λ – длина волны, а φ – начальная разность фаз.

Складываясь в точке М, колебания дадут

s = s₁ + s₂ =2a∙cos(π(d₂ –d₁)/λ + φ/2)∙cos[2π(t/T – (d₂ + d₁)/2λ) – φ/2] (6)

Таким образом, колебание в точке М имеет амплитуду, равную 2a∙cos(π(d₂ –d₁)/λ + φ/2), и интенсивность, пропорциональную

4а² cos² (π(d₂ –d₁)/λ + φ/2).

Для когерентных волн φ постоянна, и, следовательно, различие интенсивности света в разных точках зависит только от (d₂ –d₁). Благодаря этой разности расстояний или, как принято говорить, разности хода (Δ) двух волн, колебания, вызванные этими волнами в точке их встречи, будут обладать разностью фаз (ψ) даже в том случае, когда начальные фазы обеих волн были одинаковы

ψ = 2π(d₂ –d₁)/λ.

Выразим разность хода через длину волны Δ = (d₂ –d₁) = mλ, где т – любое число (целое или дробное). Соответствующая разность фаз

ψ = 2πm.

Если (φ = 0), то I A² = 4а² cos² (π(d₂ – d₁)/λ) = 4а² cos² πm. (7)

При целых т интенсивность пропорциональна 4а².

При полуцелом т интенсивность равна нулю. При этом (ψ = 2πm).

При неравных амплитудах

I A² = а₁ ² + а₂ ² + 2а₁а₂ cos 2πт = (а₁ – а₂)² + 4а₁а₂ cos² πт. (8)

При целом т имеем max – A² = (a₁ + a₂)²,

при полуцелом т – min – A² = (a₁ - a₂)².

Таким образом, геометрическое место точек пространства, характеризующихся одинаковыми амплитудами (и интенсивностями), удовлетворяет условию (d₂ –d₁)/λ = const, т. е. представляет собой поверхность гиперболоида вращения с осью S₁S₂, фокусами которого служат точки S₁ и S₂.

Для оценки видимости, или контрастности, интерференционной картины в некоторой точке интерференционного поля Майкельсон ввел параметр видимости, 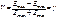где E_max и E_min –максимальная и минимальная освещенности интерференционных полос вблизи выбранной точки поля. (0 < V < 1)

Немонохроматичный свет можно представить в виде совокупности сменяющих друг друга независимых цугов. Средней продолжительностью одного цуга определяется время когерентности τ_с: если после деления волны на два пучка один из них получит временную задержку, большую продолжительности одного цуга, то такие два пучка не будут интерферировать, т. е. не будут взаимно когерентными. Поэтому когерентность существует только в пределах одного цуга и время когерентности не может превышать времени высвечивания атома, т. е. τ_с<τ. Расчеты показывают, что время когерентности и ширина спектрального интервала связаны соотношением

τ_с =l/ Δν.

Так как 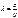, то ширина спектрального интервала, излучаемого источником света, в длинах волн .

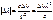Если среднюю длину волны рассматриваемого диапазона обозначить λ_ср, то , 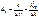. (11)

Из выражения (11) вытекает, что чем меньше спектральный интервал Δλ, т. е. чем ближе волна к монохроматической, тем больше время когерентности τ_с, а следовательно, и длина когерентности Δ_c.