Вопрос 2: Монохроматичность и когерентность.

Итак, необходимым условием интерференции волн является их когерентность, т.е. согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Этому условию удовлетворяют монохроматические волны – неограниченные в пространстве волны одной определенной и строго постоянной частоты. Так как ни один реальный источник не дает строго монохроматического света, то волны, излучаемые любыми независимыми источниками света, всегда некогерентны. Спектр частот реальной волны имеет конечную ширину 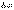. Если в какой-то момент времени волны были в фазе, через некоторое время 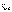разность фаз будет уже равна π (волны в противофазе). Такую волну можно приближенно считать монохроматической только в течение времени

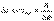За промежуток времени 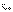разность фаз колебаний изменится на π.

Время когерентности – время, по истечении которого разность фаз волны в некоторой, но одной и той же точке пространства изменяется на π.

Волна с циклической частотой ω и фазовой скоростью распространяется за это время на расстояние

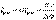, где 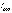– длина когерентности (длина гармонического цуга,образующегося в процессе излучения одного атома) – расстояние между точками, разность фаз в которых π. Таким образом, длина когерентности есть расстояние, при прохождении которого две или несколько волн утрачивают когерентность. Отсюда следует, что наблюдение интерференции света возможно лишь при оптических разностях хода, которые меньше длины когерентности для используемого источника света.

Чем ближе волна к монохроматической, тем меньше ширина 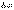и тем больше длина когерентности 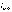, а следовательно и время когерентности .

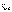Например, для видимого света ; ,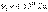

; .

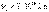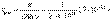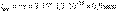Когерентность колебаний, определяемая степенью монохроматичности волн, которая совершаются в одной и той же точке пространства, называется временнóй когерентностью.

Интерференционная картина не будет наблюдаться, если максимум m-порядка для 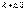будет совпадать с минимумом ( 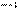)-порядка для λ. Условие неразличимости интерференционной картины:

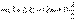, отсюда найдем критический максимум:

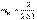. Мы можем четко наблюдать интерференционные максимумы при .

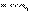Найдем связь между порядком интерференционного максимума и оптической разностью хода. Для критического максимума оптическая разность хода 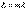, следовательно

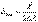, где 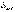– такая оптическая разность хода, при которой исчезает интерференционная картина.

Чтобы наблюдать интерференционную картину, необходимо, чтобы оптическая разность хода была много меньше длины когерентности для данного источника света: 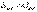, или

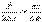. Наряду с временной когерентностью для описания когерентных свойств волн в плоскости, перпендикулярной направлению их распространения, вводится понятие пространственной когерентности. Два источника, размеры и взаимное расположение которых позволяют наблюдать интерференцию, называются пространственно-когерентными. Радиусом когерентности (или длиной пространственной когерентности) называется максимальное, поперечное направлению распространения волны расстояние, на котором возможно проявление интерференции.

Таким образом, пространственная когерентность определится радиусом когерентности:

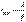,где λ – длина волны света, φ – угловой размер источника.

Для того чтобы увеличить радиус когерентности или длину пространственной когерентности, необходимо световые лучи пропускать через очень малое отверстие в непрозрачном экране А (рис. 8.2).